Пусть a, b, c различные положительные целые числа такие,
Что
b+c — a, c+a — b, a+b — с- все полные квадраты. Какое наибольшее возможное значение
может принимать a+b+c, если оно меньше 100?

Question

Математика: Пусть a, b, c различные положительные целые числа такие, Что b+c — a, c+a — b, a+b — с- все полные квадраты. Какое наибольшее возможное значение может принимать a+b+c, если оно меньше 100?

runazh · Answer

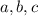Раз a,b,c попарно различны, то различны и полные квадраты. В самом деле, если 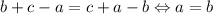$b+c-a=c+a-b \Leftrightarrow a=b$ , противоречие.

Теперь заметим, что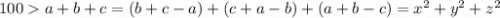 100a+b+c=(b+c-a)+(c+a-b)+(a+b-c)=x^2+y^2+z^2 . Значит, 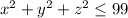$x^2+y^2+z^2\leq 99$ . Разница любых двух данных в условии квадратов четна, что говорит об одинаковой четности всех квадратов.

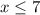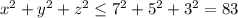Пусть — максимальное число, причем нечетное. Тогда если $x\leq 7$ , то $x^2+y^2+z^2\leq 7^2+5^2+3^2 = 83$ . Если x=9 , то $x^2+y^2+z^2\leq 9^2+3^2+1^2 = 91$ .

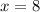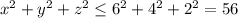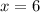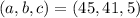Рассматривая случай четного , приходим к неравенствам $x^2+y^2+z^2\leq 8^2+4^2+2^2=84$ (соотв. x=8 ) и $x^2+y^2+z^2\leq 6^2+4^2+2^2=56$ (соотв. x=6 ). Итак, максимальное значение суммы трех квадратов равно 91. Соответствующая им тройка (a,b,c) = (45,41,5) .

Популярные вопросы