1. Математика
  2. Пусть 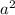= 25sin15°cos15° 1) Найдите

Пусть a^{2} = 25sin15°cos15° 1) Найдите положительное значение a
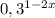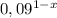2) Решите уравнение 0,3^{1-2x} + 5 · 0,09^{1-x} = a. Если уравнение имеет несколько корней, в ответ запишите их сумму

FreedomLife1 FreedomLife1    1   06.04.2021 10:16    1

Ответы
nastenka19832 nastenka19832  06.05.2021 10:21

1.

{a}^{2} = 25 \sin(15^{\circ} ) \cos(15^{\circ} ) \\ {a}^{2} = \frac{25}{2} \times 2 \sin(15^{\circ} ) \cos(15^{\circ} ) \\ {a}^{2} = \frac{25}{2} \times \sin(30^{\circ} ) \\ {a}^{2} = \frac{25}{2} \times \frac{1}{2} \\ a = \sqrt{ \frac{25}{4} } = \frac{5}{2} = 2.5

2.

{(0.3)}^{1 - 2x} + 5 \times {(0.09)}^{1 - x} = 2.5 \\ {(0.3)}^{ 1 - 2x} + 5 \times {(0.3)}^{2(1 - x)} = 2.5 \\ 0.3 \times {(0.3)}^{ - 2x} + 5 \times 0.09 \times {(0.3)}^{ - 2x} = 2.5 \\ {(0.3)}^{ - 2x} (0.3 + 5 \times 0.09) = 2.5 \\ {(0.3)}^{ - 2x} \times 0.75 = 2.5 \\ {(0.3)}^{ - 2x} = \frac{5}{2} \times \frac{100}{75} \\ {( \frac{10}{3}) }^{2x} = \frac{10}{3} \\ 2x = 1 \\ x = \frac{1}{2} \\ x = 0.5

ответ: 1)2,5 2) 0,5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
отличница459 отличница459  04.06.2020 14:02
HELP, вычислить определенный интеграл:...
эхпечальнокакто эхпечальнокакто  04.06.2020 14:01
Нужна очень Задача №1 Висота правильної трикутної піраміди дорівнює 8 см, а сторона основи 6см. Знайди бічне ребро піраміди. Задача №2 Апофема правильної трикутної піраміди...
tihomir72 tihomir72  04.06.2020 14:01
Какой функции соответствует график какой первообразной?...
lubov9 lubov9  04.06.2020 14:01
Ребят,я активно эти задания спрашиваю - не Задания 2-3 часа стоят,ну Что такое события (Достоверные,противоположные,элементарные,зависимые,независимые,полная группа)? Какова...
elenaveruaskina elenaveruaskina  04.06.2020 14:01
1588. Найдите множество натуральных решений неравенств 1) За + 2а 30.3) 8x - 5x ≤ 30;2) 4а + За ≤ 35;4) 13х - 5x 72​...
gjkbyf20061974 gjkbyf20061974  05.06.2020 13:58
Семиклассник проходит три одинаковых отрезка пути, увеличивая каждый раз время прохождения соответствующего участка пути вдвое. Скорость семиклассника на последнем отрезке...
боссмалокосоч боссмалокосоч  05.06.2020 13:57
Можете не как не могу решить......
6машка6 6машка6  05.06.2020 13:57
Ребята непонимаю один моментик в тригонометрических уравнениях там где выделено - куда пропали 2 в знаменателе и как п/6 превратилось в п/12?? обьясните плззз, может есть...
SofyaProstova SofyaProstova  05.06.2020 13:57
В коробке лежит 8 карандашей, за неделю дети изрисовали 54 карандаша. Какого наименьшего количества коробок карандашей хватит на 5 недель?...
victoriareih victoriareih  05.06.2020 13:57
Определить верные и сомнительные цифры в приближенном значении числа: а) х=55,033 ± 0,002; б) а=12*102...

Популярные вопросы