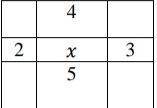
Прямоугольник четырьмя отрезками разделён на девять меньших прямоугольников, как показано на рисунке. Периметры четырёх из них известны и проставлены на рисунке внутри соответствующих прямоугольников. Чему равен периметр центрального прямоугольника, если известно, что он выражается натуральным числом и отличен от остальных указанных на рисунке периметров?

Хорошо, давайте разберемся с этой задачей.

Нам нужно найти периметр центрального прямоугольника, используя информацию о периметрах других прямоугольников.

Для начала, давайте обратим внимание на отрезки, которые делят прямоугольник на девять меньших прямоугольников. Мы видим, что каждый вертикальный отрезок делит горизонтально расположенные меньшие прямоугольники на две равные части, и каждый горизонтальный отрезок делит вертикально расположенные меньшие прямоугольники на две равные части.

Это означает, что центральный прямоугольник является пересечением двух отрезков. Давайте обозначим длину вертикального отрезка как "а" и длину горизонтального отрезка как "b".

Теперь обратимся к периметрам прямоугольников, указанным на рисунке.

Мы видим, что периметр верхнего левого прямоугольника (обозначим его как A) равен 15, периметр верхнего среднего прямоугольника (обозначим его как B) равен 20, периметр нижнего левого прямоугольника (обозначим его как C) равен 21, а периметр нижнего среднего прямоугольника (обозначим его как D) равен 16.

Мы можем использовать эту информацию для построения уравнения и решения его с помощью системы уравнений.

Начнем с верхнего левого прямоугольника. Периметр прямоугольника равен сумме всех его сторон. Так как у прямоугольника только две стороны одинаковой длины (боковые стороны), мы можем сказать, что A = 2a + b.

Точно так же, для верхнего среднего прямоугольника, B = 2a + 2b. У него две одинаковые горизонтальные стороны (сверху и снизу) и две одинаковые вертикальные стороны (слева и справа).

Аналогично, для нижнего левого прямоугольника, C = 2a + 2b.

Наконец, для нижнего среднего прямоугольника, D = 2b + a.

Теперь у нас есть система уравнений:

A = 2a + b
B = 2a + 2b
C = 2a + 2b
D = 2b + a

Мы можем использовать эти уравнения, чтобы решить их относительно переменных "a" и "b". Давайте начнем с уравнений A и B.

Вычтем уравнение А из уравнения B:

B - A = (2a + 2b) - (2a + b)
B - A = 2b - b
B - A = b

Теперь, добавим уравнение C к уравнению D:

C + D = (2a + 2b) + (2b + a)
C + D = 3a + 4b

Теперь у нас есть следующие уравнения:

B - A = b
C + D = 3a + 4b

Мы хотим найти периметр центрального прямоугольника, что можно выразить через переменные "a" и "b". Давайте обозначим его как "P".

Периметр центрального прямоугольника равен 2a + 2b, что можно записать как P = 2a + 2b.

Теперь, используя систему уравнений, мы можем решить два уравнения для двух неизвестных переменных "a" и "b", а затем подставить их в уравнение для периметра центрального прямоугольника.

Заменим "b" в уравнении B - A на (C + D)/4:

B - A = (C + D)/4

Используем уравнение C + D = 3a + 4b и подставим его в уравнение B - A:

B - A = (3a + 4b)/4

Теперь решим это уравнение относительно "a":

(3a + 4b)/4 = B - A

3a + 4b = 4B - 4A

3a = 4B - 4A - 4b

a = (4B - 4A - 4b)/3

Теперь используем значение "a" для вычисления значения "b" из уравнения C + D = 3a + 4b:

C + D = 3a + 4b

C + D = 3((4B - 4A - 4b)/3) + 4b

C + D = 4B - 4A - 4b + 4b

C + D = 4B - 4A

Используем полученные значения "a" и "b" для вычисления периметра центрального прямоугольника:

P = 2a + 2b

Подставим значения "a" и "b":
P = 2((4B - 4A - 4b)/3) + 2b

Когда мы упростим это уравнение, получим итоговое значение периметра центрального прямоугольника.

Исходя из этих шагов решения, вы сможете самостоятельно сделать все расчеты и найти ответ на задачу. Удачи!