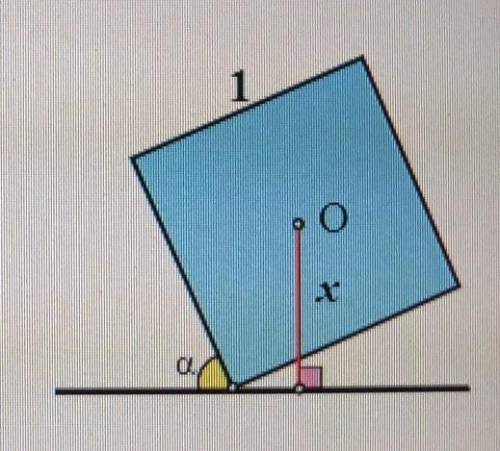
Прямая проходит через вершину квадрата и образует с его стороной угол alpha. Найдите расстояние до
этой прямой от центра квадрата, если его сторона
равна
1, а ѕіn alpha = 0, 8.​

Для решения данной задачи нам понадобится использовать геометрические знания и формулы для нахождения расстояния от точки до прямой.

Для начала, построим рисунок и обозначим величины, чтобы было проще представить себе задачу. По условию, у нас имеется квадрат, сторона которого равна 1. Прямая проходит через одну из его вершин и образует с его стороной угол α.

Так как sin α = 0.8, мы можем найти значение угла α с помощью арксинуса. Используя калькулятор, найдем, что α = arcsin(0.8) ≈ 53.13°.

Теперь, чтобы найти расстояние от центра квадрата до этой прямой, нам понадобится формула для нахождения расстояния от точки до прямой:

d = |Ax + By + C| / √(A^2 + B^2),

где A, B и C - это коэффициенты уравнения прямой, а x и y - координаты точки.

В данном случае, прямая проходит через вершину квадрата, поэтому ее уравнение может быть представлено в виде y = kx, где k - угловой коэффициент.

Угловой коэффициент можно найти, используя формулу tg α = k. Так как tg α = sin α / cos α, то k = sin α / cos α.

Так как прямая проходит через вершину квадрата, координаты ее точки равны (1, 1), и уравнение прямой будет иметь вид y = (sin α / cos α)x + 1.

Далее, найдем значения A, B и C для нашей прямой, зная ее уравнение. Здесь A = (sin α / cos α), B = -1 и C = -1.

Теперь мы можем использовать формулу для нахождения расстояния от центра квадрата до прямой:

d = |(sin α / cos α) * (0) + (-1) * (0) + (-1)| / √((sin α / cos α)^2 + (-1)^2).

Упростим это выражение:

d = |-1 / cos α| / √((sin α / cos α)^2 + 1).

Теперь вставим значение sin α и α в формулу и рассчитаем расстояние:

d = |-1 / cos(arcsin(0.8))| / √((sin(arcsin(0.8)) / cos(arcsin(0.8)))^2 + 1).

d = |-1 / cos(53.13°)| / √((0.8 / cos(53.13°))^2 + 1).

Используя калькулятор, рассчитаем значение этого выражения:

d ≈ 1.66.

Таким образом, расстояние от центра квадрата до прямой примерно равно 1.66 (округленно до двух знаков после запятой) единицы длины.