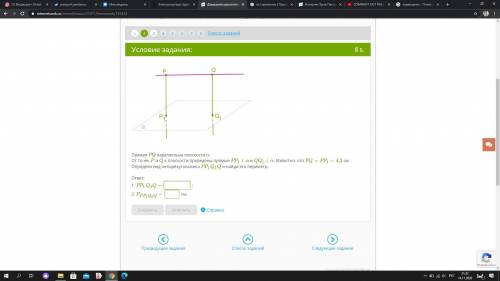
Прямая PQ параллельна плоскости α. От точек P и Q к плоскости проведены прямые PP1⊥α и QQ1⊥α. Известно, что PQ=PP1=4,3 см.
Определи вид четырёхугольника PP1Q1Q и найди его периметр.

Для решения данной задачи нам потребуется знание основных свойств параллелограмма, так как четырехугольник PP1Q1Q является параллелограммом.

Поскольку сторона PQ параллельна плоскости α, то стороны PP1 и QQ1 будут перпендикулярны плоскости α.

Из условия задачи известно, что PQ = PP1 = 4,3 см. Это означает, что сторона PP1 равна 4,3 см.

Так как сторона PP1 перпендикулярна плоскости α, то она будет перпендикулярной к стороне PQ. Поэтому треугольник PP1Q будет прямоугольным треугольником, где PP1 будет гипотенузой, а PQ и QP1 будут катетами.

Теперь мы можем применить теорему Пифагора для нахождения стороны QP1:
QP1^2 = PQ^2 - PP1^2
QP1^2 = (4,3)^2 - (4,3)^2
QP1^2 = 18,49 - 18,49
QP1^2 = 0
QP1 = 0

Из этого следует, что сторона QP1 имеет нулевую длину, а значит, она является точкой Q. Следовательно, четырехугольник PP1Q1Q является треугольником PP1QQ1.

Теперь мы можем найти периметр данного треугольника. Периметр треугольника равен сумме длин его сторон.

Периметр = PP1 + QQ1 + Q1P
Так как QQ1 перпендикулярна плоскости α, то она будет равна длине стороны QQ. Также, так как QP1 имеет нулевую длину, то Q1P будет равна длине стороны P1Q.

Периметр = 4,3 см + QQ + P1Q

Так как четырехугольник PP1Q1Q является параллелограммом, то его стороны PP1 и Q1Q будут равны.

Периметр = 4,3 см + QQ + 4,3 см

Однако, у нас нет информации о длине стороны QQ, поэтому мы не можем найти точное значение периметра треугольника PP1QQ1. Мы можем только сказать, что периметр равен 8,6 см + QQ.

С данными, которые у нас есть сейчас, мы не можем найти точный периметр треугольника. Для этого нам необходимо знать дополнительные данные, например, длину стороны QQ или угол между стороной PQ и плоскостью α.