Прямая l1 задана общим уравнением. Найдите неизвестный параметр канонического уравнения прямой l2, перпендикулярной прямой l1.
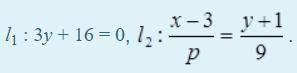
Другие вопросы по теме Математика
Популярные вопросы
- Придумать страшную и мистическую , нам в школе задали по . я не то хочу, что бы...
1 - Биссектриса угла а параллелограмма abcd пересекает сторону bc в точке e. найдите...
2 - Объяснить постановку знаков препинания только теперь он, видно, понял, как велика...
3 - Найдите значение выражения два умножить на два в пятой степени минус три в третьей...
1 - Что понимается содружеством? что ты об этом знаешь?...
2 - Выпиши слова в которых корень совпадает с основой? парк свет секрет чашечка кораблик...
3 - Написать не большой рассказ растения в моем доме...
2 - На берегу лены горы, еще не освещенные солнцем, выделялись на посветлевшем небе....
1 - Чому рептилій ще називають плазунами ?...
3 - Сочинение на тему: что я знаю о словарях...
1
Изображенная на рисунке прямая l1 имеет угол наклона к оси OX, то есть касательную тангенсом угла наклона. Из рисунка видно, что тангенс угла наклона прямой l1 равен m = 5/3.
Таким образом, уравнение прямой l1 можно записать как y = (5/3)x + b, где b - это неизвестный параметр.
Теперь нам нужно найти каноническое уравнение прямой l2, которая будет перпендикулярна прямой l1.
Для этого нам понадобятся свойства перпендикулярных прямых:
1. Угол наклона перпендикулярных прямых является обратным по знаку к углу наклона исходной прямой. Так как угол наклона прямой l1 равен 5/3, угол наклона прямой l2 будет равен -3/5.
2. Перпендикулярные прямые имеют противоположные взаимные коэффициенты перед x и y в их каноническом уравнении. То есть, если уравнение прямой l1 имеет вид y = mx + b, то уравнение перпендикулярной прямой l2 будет иметь вид y = (-1/m)x + c, где c - это новый неизвестный параметр.
В нашем случае, уравнение прямой l2 будет иметь вид y = (-1/(-3/5))x + c, что равносильно y = (5/3)x + c.
Таким образом, нам необходимо найти значение параметра c в уравнении прямой l2.
Но, поскольку у прямых l1 и l2 есть общую точку пересечения, что отличает их линейно зависимыми, их канонические уравнения совпадают. То есть, коэффициенты при x и y в уравнениях l1 и l2 должны быть одинаковы.
Таким образом, (5/3)x + b = (5/3)x + c.
Для удобства можно сократить (5/3)x, получив b = c.
То есть, неизвестный параметр канонического уравнения прямой l2 равен параметру b из уравнения прямой l1.