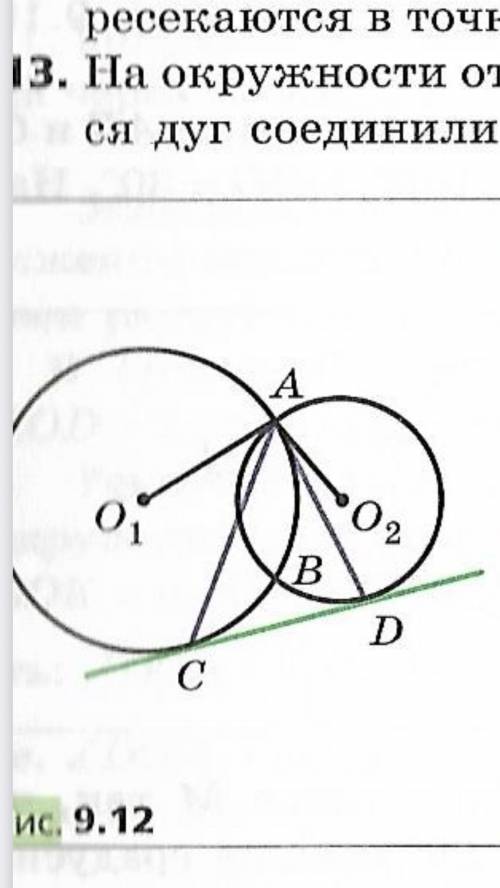
прямая касается двух окружностей с центрами о1 и о2 в точках с и д соответственно А и В точки пересечения окружностей.Найдите угол о1а02,если угол САD равен а.

2α

Пошаговое объяснение:

Для решения данной задачи, нам понадобятся определенные геометрические свойства.

1. Свойство касательной: Угол между касательной и радиусом, проведенным в точку касания, равен 90 градусов. То есть ∠O1AC = 90° и ∠O2BD = 90°.

2. Четырехугольник ABCD: Для четырехугольника ABCD с противоположными сторонами AD и BC, сумма внутренних углов равна 360 градусов. То есть ∠BAD + ∠CDA + ∠DCB + ∠CBA = 360°.

Теперь приступим к решению задачи.

У нас дано, что угол CAD равен а. Давайте обозначим его этой буквой: ∠CAD = а.

Из свойства касательной, у нас есть следующие равенства:
∠O1AC = 90° и ∠O2BD = 90°.

Также у нас есть противоположные углы, образованные касательными: ∠CAB и ∠BDC.

Заметим, что угол BAD (оставшаяся часть угла CAD) образован противоположными углами в четырехугольнике ABCD и равен 180° - а (внутренний угол четырехугольника ABCD).

Теперь рассмотрим треугольники ∠O1AC и ∠O2BD. Эти треугольники подобные, так как у них углы ∠O1AC и ∠O2BD прямые (90°) и у них общий угол ∠CAD = а.

Из подобия треугольников, мы можем записать следующие отношения между соответствующими сторонами:

(OC1/O2B) = (AC1/BD)

Из свойства радиусов, мы знаем, что OC1 = OC2 (радиусы окружностей), поэтому можно обозначить радиусы как R:

(R/R2) = (AC1/BD)

Теперь рассмотрим прямоугольный треугольник CBD. Мы знаем, что угол ∠CBD = 90° (так как DCB - это касательная), а угол BCD имеет меру 180° - а (противоположный угол в четырехугольнике ABCD). Таким образом, угол BCD имеет меру 180° - а.

Теперь мы можем записать соотношение между BD и BC:

BD/BC = sin(180° - а)

Так как ∠O2BD = 90°, треугольник O2BD - прямоугольный и можно использовать теорему синусов, чтобы получить отношение между BD и BC:

BD/BC = sin(BDC)/sin(BCD)

Подставим вместо sin(BCD) значение, полученное ранее:

BD/BC = sin(BDC)/sin(180° - а)

Из подобия треугольников ∠O1AC и ∠O2BD, мы также знаем, что

AC1/BD = sin(второй угол треугольника O1AC) / sin(второй угол треугольника O2BD)

Но так как ∠O1AC = 90° и ∠O2BD = 90°, то получаем:

AC1/BD = sin(90°) / sin(90°) = 1/1 = 1

То есть AC1/BD = 1.

Теперь объединим все полученные соотношения:

1 = sin(BDC)/sin(180° - а)

sin(BDC) = sin(180° - а)

sin(BDC) = sin(180°)cos(а) - cos(180°)sin(а)

sin(BDC) = 0 - (-1)sin(а) = sin(а)

Из этого следует, что угол BDC равен а.

Но мы также знаем, что угол BAD = 180° - а.

Теперь рассмотрим треугольник O1CA0. Угол O1CA0 (обозначим его как β) получается путем суммы углов O1CA = 90° + ∠CAD (то есть 90° + а) и ∠A0CD = ∠BDC (то есть а). Таким образом, угол O1CA0 (β) равен (90° + а) + а = 90° + 2а.

Итак, мы нашли, что угол O1CA0 равен 90° + 2а.