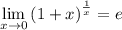Проверьте правильность решения lim-> 0(1/x+1)^1/2x=1/lim-> 0(1+1/x)^1/x×x×1/2x=1/√е
Другие вопросы по теме Математика
Популярные вопросы
- Выражение (a^2 – 2b)(b – 3a^2) а– 3a4 + 7a2b – 2b2; б – 3a4 – 5a2b – 2b2; вa2 –...
2 - Каким образом в лист поступает углекислый газ для фотосинтеза...
2 - 5. второстепенный член предложения, обозначающий признак предмета и отвечающий на...
1 - Написать сочинение на тему : что было бы если исчезла сила трения ?...
2 - При изменении силы тока в электромагните из 2.9 к 9.2а энергия магнитного поля изменилась...
1 - Діагональ правильної чотирикутної призми нахилена до площини основи під кутом 60....
1 - Какой частью речи является слово дважды ? нужно ! !...
3 - 5ab-7b+5a²-7a сначала нужно решить рациональным потом подставить a=3,7; b=-3,7...
2 - Какими числами можно заменить звёздочку, чтобы точка с (*; -5) принадлежала четвёртому...
3 - При каком значении х вектора а(-2: 6) и b(x; -3) будут перпендикулярными? а) -9...
3
Здесь неопределенность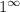 , следовательно, нужно применить второй замечательный предел
, следовательно, нужно применить второй замечательный предел