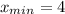Производная функции y=5^{x}^{2} имеет вид: а) y'5^{x}^{2} ln 5; б) y'=x^{2}5^{x}^{2-1}; в) y'= 2x5^{x}^{2} ln x^{2}; г) y'= 2x5^{x}^{2} ln 5 2.Точкой минимума функции y=\frac{1}{3} x^{3}-2x^{2} является: а) нет экстремума; б) -2; в) 4; г) 0 3. Вторая производная функции y=1-2x+4x^{2} имеет вид: а) y''=-2x+8; б) y''=3; в) y''=8 г) y''=0
Другие вопросы по теме Математика
Популярные вопросы
- . катеты прямоугольного треугольника равны 12 см и 7 см найти площадь...
2 - Записати шлях героя до корабля ( твір жага до життя). ів...
1 - Написать отзыв на одно из прочитанных произведений (Лермонтов, Гоголь,...
1 - Описать художественное пространство повести в хронологическом порядке...
1 - Обчислити масу заліза, що використали для отримання 185 г ферум(ІІІ)...
3 - «Пісня про Роланда» Прочитай уривок художнього тексту та виконай завдання:...
2 - Продолжи предложение Ночью выпал снег и...
3 - Сөйлемді аяқта. Күн куркереген сайын өзімді жайсыз...
1 - РЕШИТЕ , УЖЕ 1 ЧАС НЕ ПОНИМАЮ,...
3 - 151 задача, желательно с дано и с рисунком...
2
В точке минимума производная меняет знак с "-" на "+"
⇒