Произведение цифр натурального двузначного числа равно 5, а сумма квадратов цифр этого
числа равна 26. Найдите сумму таких чисел.
Другие вопросы по теме Математика
Популярные вопросы
- Найдите значение выражения 1,5*10^2/ 3*10^-1...
1 - 3целых2/5 / х = 6целых4/5 : 1целых1/3...
2 - Вкаждом случае восстанони полную запись деления в столбик 361286: 7,25687:...
3 - Какая плотность хозяйственого мыла? напишите решение...
3 - Образуйте от глаголов дейст. причастия настоящего времени , составьте...
3 - Треть числа равна 39 .найдите это число.-13. 42. 78. 117....
1 - Какое значение для формирования государства имел путь из варяг в греки?...
3 - Какие новые черты личности гринева раскрываются в сцене разговора с...
2 - Найдите корни уравнения(9кл) x^2-7x+6 = 0 x^3-2x^2+1...
2 - Пригадайте як відбувається купівля наприклад книги(відео-диска)в магазині...
1
Сумма таких чисел равна 66.
Пошаговое объяснение:
Чтобы в произведении цифр натурального числа было число 5, эти цифры должны быть 1 и 5. Сумма их квадратов равна 1 * 1 + 5 * 5 = 26. Существует два таких числа: 15 и 51. Их сумма равна 15 + 51 = 66.
66
Пошаговое объяснение:
Пусть x - десятки, а y - единицы.
Тогда:
При этом все число - это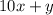 .
.
Решим систему уравнений:
Поскольку натуральные числа не дают в сумме отрицательное значение, вторую систему не рассматриваем.
Тогда останется:
Тогда имеем 2 числа, которые удовлетворяют условию:
Найдем их сумму: