Проинтегрировать дифференциальные уравнения первого порядка a) xlnx*y' - y = 0
b) y' – 3y = е^5х + 7
Другие вопросы по теме Математика
Популярные вопросы
- Скласти психологічний портрет героя через знакову систему імені...
3 - Запиши выражения по задачам.а) Для сохранения тюленей в Каспийском...
1 - Кластер на тему повседневная жизнь населения , история 6 класс...
3 - K2SO4+BaCl2= BaSO4+ 2KCl тип реакции...
2 - Придумати задачу: Раціональні та від ємні...
3 - 3. Величина заряда через электролит, уменьшилась на 60%. Во сколько...
3 - Всё самое хорошее о весне кратко ...
1 - Побудуйте графік функції, заданої формулою:а) у = х – 2; б) у =...
1 - 6. Как связаны между собой tg a, sin a и cos a? 7. Как связаны между...
3 - Решить кроссворд про волков...
3
а)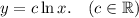
б)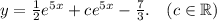
Пошаговое объяснение:
а) Начнём с классификации ДУ. Это ДУ первого порядка, первой степени, линейное, обыкновенное.
В таком случае подойдёт замена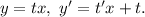 Введём её:
Введём её:
Удалось разделить переменные. Проинтегрируем обе части уравнения:
Приравняем и упростим обе части уравнения:
Обратная замена:
Логарифм от существует только тогда, когда
существует только тогда, когда 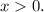 Модуль
Модуль 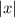 для
для 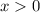 равен самому
равен самому  , поэтому:
, поэтому:
б) Начнём с классификации ДУ. Это ДУ первого порядка, первой степени, линейное, обыкновенное.
Введём переменную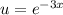 и домножим на неё обе части уравнения:
и домножим на неё обе части уравнения:
Отметим, что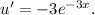 Зная это, упростим:
Зная это, упростим:
Удалось разделить переменные. Проинтегрируем обе части уравнения:
Обратим замену, приравняем выражения и упростим: