Профильная математика 13 задание Решаю для себя сборник 2018г
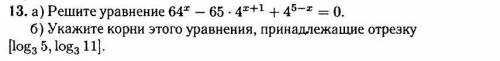
Другие вопросы по теме Математика
Популярные вопросы
- Отредактируйте предложения с деепричастиями. В чём причина ошибок? 1. Возвращаясь...
2 - Прочитайте текст и озаглавьте его. По засыпанному галькой берегу шли три...
1 - К каким частям речи относятся выделенные слова? На какие вопросы они отвечают...
3 - К каким частям речи относятся выделенные слова? Приведите доказательства....
3 - Прочитайте выразительно отрывок. Вспомним с нами отступавших, Воевавших...
3 - Прочитайте пословицы. Понятен ли их смысл? 1. Молчащий в правом деле подобен...
2 - Рассмотрите опорный материал. Какие типы орфограмм есть в русском языке?...
2 - Объясните орфограммы в корнях слов и подготовьтесь писать под диктовку....
2 - Пользуясь алгоритмом действий в опорном материале, объясните выбор гласных...
2 - Дополните таблицу своими примерами. В третью графу подберите слова с корнями,...
3
Пошаговое объяснение:
Умножим обе части уравнения на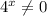 :
:
по теореме Виета:
а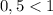 , значит,
, значит, 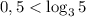 и
и ![0,5 \notin [\log_3{5};\log_3{11}]](/tpl/images/1358/5602/00d12.png)
13. а) Если 4ˣ=у>0, то у³-65у*4+4⁵/у=0; у⁴-65*4у²+4⁵=0, получили биквадратное уравнение. у²=65*2±√(16900-1024)=130±√(15876)=130±126; у²=256; у²=-16;∅у²=16;
у²=4; у=-2; ∅;у=2; 4ˣ=16⇒х=2; 4ˣ=2⇒х=1/2;
ответ 2; 1/2
б) 2=㏒₃3²=㏒₃93; 1/2=㏒₃√3
2= ㏒₃9∈ [㏒₃5; ㏒₃11]
1/2=㏒₃√3∉[㏒₃5; ㏒₃11]
б)ответ 2