Продолжения медиан AM и BK треугольника ABC пересекают описанную около треугольника ABC окружность omega в точках N и L соответственно. Найдите площадь треугольника ABC, если радиус окружности omega равен 17, AN : AM = 1,8, ~BL : BK = 2 : 1.
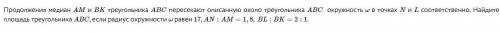
Другие вопросы по теме Математика
Популярные вопросы
- ( ответьте на все: 12,13,14)...
2 - Мәтін бойынша тудың әр элементінің мағынасын суретке жазыныз 13 ба 1....
3 - Дайте характеристику территории государства абулхаирского ханства Абулхаирское...
3 - А) Тұз қышқылы (HCl) молекуласындағы ковалентті байланыстардың түзілу...
3 - Спираль электрической плитки изготовлена из никелиновой проволоки, длина...
2 - Закончите следующие уравнения реакций: 1) Zn(NO3)2 → 2) Ni(NO3)2 → 3)...
3 - Көмектесіңдерші тжб 6сынып Қазақ тілінен...
2 - 5 Song: Read the song and complete the gaps with the words below.Then,...
2 - Что такое конфликт и как из него выйти.привет я Вася!...
1 - Дайте полное описание этой части света по плану: 1) название части света...
2
AM– медиана Δ АВС, значит BM=MC, M – середина ВС.
ВK– медиана Δ АВС, значит AK=KC, K – середина АС.
Значит KM – средняя линия Δ АВС:
KM || AB
KM=(1/2)AB.
По условию AE:AM=2:1 ⇒ AM=ME и M – середина AE
Значит, KM – средняя линия Δ АСЕ:
KM || СЕ
KM=(1/2)СЕ.
AB || KM || CE ⇒ AB || CE
б)
AB=CE=2KM
Значит и дуги АВ и СЕ, стягиваемые равными хордами равны.
рис.3
∠САЕ= ∠ BCA как углы, опирающиеся на равные дуги.
Δ АМС – равнобедренный.
MС=MA.
Так как
MA=ME, то
MC=MA=ME и поэтому
M– центр окружности, описанной около треугольника АСЕ.
а значит и около треугольника АВС.
MС=MB
MC=MA
MC=MB=MA
∠ A=90o
BC и АЕ – диаметры.
Обозначим MC=MB=MA=ME=R
KF=x, по условию BF:BK=2:3 , значит BK=2x
Медианы АМ и BK пересекаются в точке D.
AD:DM=2:1
BD:DK=2:1
AD=(2/3)R; DM=(1/3)R
BD=(4/3)x; DK=(2/3)x
DF=DK+KF=(2/3)x+x=(5/3)x
DE=DM+ME=(1/3)R+R=(4/3)R
По свойству пересекающихся хорд:
BD·DF=AD·DE
(4/3)x·(5/3)x=(2/3)R·(4/3)R
x2=(2/5)R2
Из Δ MDB по теореме косинусов:
DB2=MD2+MB2–2MD·MB·cos ∠ BMD
⇒
cos ∠ BMD=((R/3)2+R2–(4/3x)2)/(2·(R/3)·R)=
=((10R2/9)–(16/9)·(2/5)R2)/(2·R2/3)= (18/45)·(3/2)=0,6
По теореме косинусов из Δ АМВ
АВ2=R2+R2–2R·R·0,6
AB=R·√0,8
sin ∠ C =AB/CB=√0,8/2=√0,2=1/√5
∠ C= arcsin(1/√5)
sin ∠ B= cos ∠ C= 2/√5
∠ B= arcsin(2/√5)
tg∠ B=sin∠ B/cos∠ B=2; tg∠ C=1/2
О т в е т. 90o; arcsin(1/√5);arcsin(2/√5)
или
90o; arctg2 и arctg(1/2)
Условие
Продолжения медиан AM и BK треугольника ABC пересекают описанную около него окружность в точках E и F соответственно, причём AE:AM=2:1 , BF:BK=3:2 . Найдите углы треугольника ABC .
Решение
Диагонали BC и AE четырёхугольника ABEC точкой пересечения M делятся пополам, значит, этот четырёхугольник – параллелограмм, а т.к. он вписан в окружность, то это прямоугольник. Следовательно, BAC = 90o . Пусть FK=t , BK=2t , AK=KC=x . По теореме о произведениях отрезков пересекающихся хорд AK· KC=BK· KF , или x2=2t· t = 2t2 , откуда x=t . Из прямоугольного треугольника ABK находим, что
sin ABK = = = = ,
поэтому ABK = 45o . Тогда AB=AK=x . Следовательно,
tg ABC = = = 2.
ответ
90o , arctg 2 , 90o- arctg 2 .
Источники и прецеденты использования