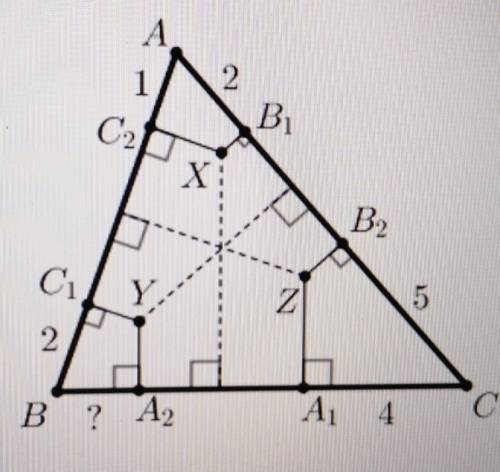
Про треугольник ABC известно, что AB=6, AC=9, BC=8. На его сторонах выбраны точки A1, A2, B1, B2, C1, C2, как показано на рисунке. Перпендикуляры, восстановленные в точках B1 и C2 к сторонам, на которых они лежат, пересекаются в точке X. Аналогично определяются точки Y и Z. Известно, что перпендикуляры, опущенные из X на BC, из Y на AC и из Z на AB пересекаются в одной точке. Чему равна длина отрезка BA2, если AC2=1, AB1=2, CB2=5, CA1=4, BC1=2?​

badangel888    2   16.10.2020 07:22    17