Про натуральные числа m и n известно, что m^2+m+n^2 делится на mn. докажите, что m - точный квадрат

Если m=1, то m является полным квадратом (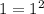), поэтому этот случай можно не рассматривать.

Пусть m>1 не является полным квадратом, тогда в разложении m на простые множители (существование такого разложения гарантируется основной теоремой арифметики)

хотя бы один показатель является нечетным числом. Не теряя общности, можно предположить, что это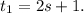

По условию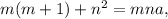 где a - целое число. Разделим это равенство на m:

Поскольку m+1 и na - целые числа,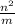 является целым числом, то есть 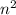делится на m, откуда 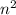делится на 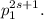Отсюда следует, что n делится на 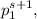следовательно 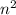делится на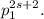

Теперь мы уже на финише. Из последнего рассуждения следует, что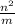 делится на 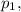na, естественно, делится на 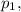но (m+1) ну никак не может делиться на 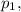поскольку соседние натуральные числа взаимно просты (а m делится на ).

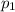Полученное противоречие доказывает, что m обязано быть полным квадратом.