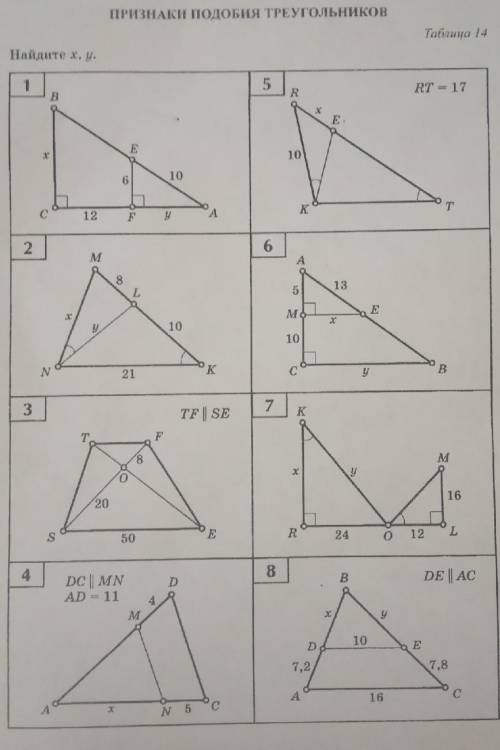
Признаки подобия треугольников таблица 14 по геометрии 8 класс. Решите задачу под номером 1,5,6,8​

Хорошо, я приведу пошаговое решение для задач под номерами 1, 5, 6 и 8, используя признаки подобия треугольников.

Задача 1:

В задаче дано, что треугольники ABC и DEF подобны. Нам нужно определить, какие стороны треугольника DEF подобны сторонам треугольника ABC.

1. По определению подобия треугольников, соответствующие углы треугольников равны.
Угол A равен углу D, угол B равен углу E и угол C равен углу F.

2. Сравним соответствующие стороны треугольников. По условию задачи, сторона AB подобна стороне DE.

Ответ: Сторона AB подобна стороне DE.

Задача 5:

В задаче дано, что треугольники ABC и XYZ подобны. Нам нужно найти значение выражения (XY / BC) + (XZ / AC).

1. По определению подобия треугольников, соответствующие углы треугольников равны.
Угол A равен углу X, угол B равен углу Y и угол C равен углу Z.

2. Сравним соответствующие стороны треугольников. По условию задачи, сторона BC подобна стороне XZ и сторона AC подобна стороне XY.

3. Вставим значения сторон BC и AC в выражение и упростим:
(XY / BC) + (XZ / AC) = (XY / XZ) + (XZ / XY) = (XY^2 + XZ^2) / (XY * XZ)

Ответ: Значение выражения (XY / BC) + (XZ / AC) равно (XY^2 + XZ^2) / (XY * XZ).

Задача 6:

В задаче дано, что треугольники ABC и XYZ подобны. Нам нужно доказать, что отношение площадей треугольников ABC и XYZ равно квадрату отношения соответствующих сторон.

1. По определению подобия треугольников, соответствующие углы треугольников равны.
Угол A равен углу X, угол B равен углу Y и угол C равен углу Z.

2. Сравним соответствующие стороны треугольников. По условию задачи, сторона AB подобна стороне XY, сторона AC подобна стороне XZ и сторона BC подобна стороне YZ.

3. Доказательство:
Пусть S1 - площадь треугольника ABC и S2 - площадь треугольника XYZ.
Тогда мы хотим доказать, что S1 / S2 = (AB / XY)^2 = (AC / XZ)^2 = (BC / YZ)^2.

Из подобия треугольников следует, что AB/XY = AC/XZ = BC/YZ (соотношение подобия сторон).
Тогда (AB / XY)^2 = (AC / XZ)^2 = (BC / YZ)^2.

Таким образом, мы доказали, что отношение площадей треугольников ABC и XYZ равно квадрату отношения соответствующих сторон.

Задача 8:

В задаче дано, что треугольники ABC и DEF подобны. Нам нужно найти пропорцию между длинами сторон треугольников.

1. По определению подобия треугольников, соответствующие углы треугольников равны.
Угол A равен углу D, угол B равен углу E и угол C равен углу F.

2. Сравним соответствующие стороны треугольников. По условию задачи:
AB/DE = BC/EF = AC/DF.

Ответ: Пропорция между длинами сторон треугольников ABC и DEF равна AB/DE = BC/EF = AC/DF.

Надеюсь, это решение понятно и поможет вам понять, как применять признаки подобия треугольников в геометрии.