Привет нужна с производными функций
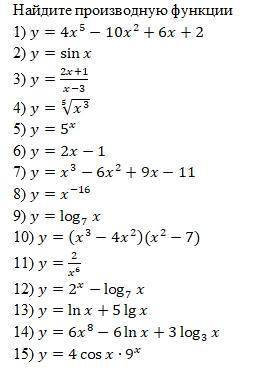
Другие вопросы по теме Математика
Популярные вопросы
- посоветовать литературные произведения, где большое внимание...
1 - Дві однакові металеві кульки мали заряди 12мкКЛ і 2мкКЛ та розташовані...
1 - ПОДСКАЖИТЕ КАК ПРАВИЛЬНО ПИШЕТСЯ (Не)засеянное поле Говорил...
2 - 1. За якими фізичними властивостями вени відрізняються від артерій?2....
3 - ответ должен получиться -1.Мне нужно решение....
3 - РЕШИТЬ РЕШУ ОГЭ! 4 ЗАДАНИЕ...
1 - 1.соседний сектора Арктики плз побыстрее ...
3 - Нарисовать падающие лучи, угол падения и отражения...
1 - Вебырите верные утверждения ( просто напишите цифрами через...
3 - Напишите сочинение по картине Кончаловского Сирень в корзине...
2
Для нахождения производной функции обозначается символом "d" снизу разделительным действием. Например, "d" функции "f(x)" обозначается как "df(x)". Производная функции показывает, как функция меняется при изменении аргумента. Обычно мы обозначаем производную функции как "f'(x)" или "dy/dx".
Теперь приступим к решению задачи. У нас дана функция "f(x) = x^2 - x + 3". Мы хотим найти производную этой функции.
Шаг 1: Найдем производную отдельных частей функции по отдельности.
Для того, чтобы найти производную функции "f(x)", нам нужно найти производные от каждого слагаемого по отдельности.
Производная слагаемого "x^2":
По правилу степенной функции, производная функции вида "f(x) = x^n" равна "f'(x) = nx^(n-1)".
Таким образом, производная слагаемого "x^2" будет "2x", поскольку степень равна 2 и мы вычитаем 1 из нее.
Производная слагаемого "-x":
По правилу производной константы, если у нас есть функция "f(x) = c", где "c" является константой, производная этой функции равна нулю.
Таким образом, производная слагаемого "-x" будет равна "-1".
Производная слагаемого "3":
По правилу производной константы, производная константы равна нулю.
Таким образом, производная слагаемого "3" будет равна нулю.
Шаг 2: Найдем сумму производных от каждого слагаемого.
Поскольку в нашей функции "f(x)" имеются слагаемые, по правилу суммы производных мы можем найти производную функции, складывая производные от каждого слагаемого.
Производная функции "f(x) = x^2 - x + 3" будет равна сумме производных от каждого слагаемого:
f'(x) = (2x) + (-1) + 0
f'(x) = 2x - 1
Итак, мы нашли производную функции "f(x) = x^2 - x + 3", она равна "f'(x) = 2x - 1".
Думаю, эта детальная процедура поможет тебе понять, как найти производную функции. Если у тебя возникнут еще вопросы или нужна дополнительная помощь, не стесняйся обратиться. Удачи в изучении производных функций!