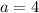Прикаких значениях параметра a произведение действительных корней уравнения x2−(a+3)x+a2−7=0 на 2 больше суммы этих корне?

Корни -3 и 4 НЕ правильные

Воспользуемся теоремой Виета:

Произведение корней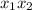 на 2 больше суммы 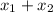этих корней, следовательно:

Определим, при каких значениях параметра данное уравнение существует.

Следовательно,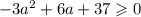 — условие существования корней данного квадратного уравнения.

Проверим, удовлетворяют ли полученные значения параметров для решения исходного уравнения.

Если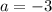 , то получаем неправильное неравенство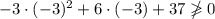

Если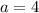 , то получаем верное неравенство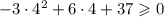

Таким образом, только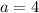 обратит данное уравнение в таковое, что произведение корней на 2 будет больше суммы этих корней.

ответ: