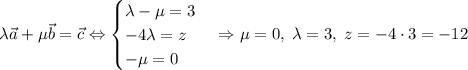При каком значении z векторы a{1;-4;0}, b{-1;0;-1} и c{3;z;0} компланарны?
Другие вопросы по теме Математика
Популярные вопросы
- Как называлось объединение казачьих поселений, казацкая республика, возникшая...
2 - Одной из причин Великих географических открытий было стремление европейцев...
2 - Основным занятием большинства населения России в XVI в. было(-а)...
3 - Какая страна из перечисленных в результате географических открытий стала...
2 - Мореплаватель Христофор Колумб, отправляясь в первое путешествие, находился...
1 - Одна из особенностей России, вследствие которой страна была позднее вовлечена...
2 - Отметьте одно из отрицательных последствий Великих географических открытий....
2 - Как назывались морские парусные суда нового типа, на которых отправлялись...
1 - В каком веке русский купец Афанасий Никитин совершил своё путешествие в страны...
2 - Назовите сочинение тверского купца Афанасия Никитина, в котором он описывал...
1
Векторы компланарны тогда и только тогда, когда их смешанное произведение равно .
.
Есть и другой . Как видно, векторы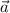 и
и 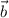 неколлинеарны, а потому вектор
неколлинеарны, а потому вектор 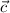 можно представить в виде линейной комбинации этих векторов тогда и только тогда, когда
можно представить в виде линейной комбинации этих векторов тогда и только тогда, когда 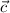 лежит в одной плоскости с данными векторами. Иными словами:
лежит в одной плоскости с данными векторами. Иными словами: