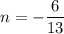При каком значении n вектора а(1;2n+1), b(n;6):
A) равны
В) коллинеарный
С) перпендикулярны
Другие вопросы по теме Математика
Популярные вопросы
- Какие изобретения человека появлению и развитию науки цитологии?...
1 - Поясните, почему микробиология изучает главным образом бактерий....
2 - Почему клеточный цикл жизни начинается с деления и оканчивается...
1 - В 1992 г. на конференции ООН по окружающей среде в Рио-де-Жанейро...
3 - Поясните, какие функции в ядре выполняет хроматин....
1 - Почему у водорослей много разных форм полового процесса?...
2 - Заполните таблицу по предложенной схеме: а) впишите названия...
3 - Поскольку цианобактерии, обладая хлорофиллом к фотосинтезу,...
3 - Охарактеризуйте роль ядра в жизнедеятельности клетки....
1 - Поясните, в чём выражается опасность внесения прокариотных препаратов...
3
А) Два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
➠ В) Вектора коллинеарные, если их координаты пропорциональны:
➠ Равные длины:
Так как нет таких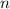 , при которых вектора
, при которых вектора 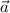 и
и 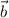 одновременно коллинеарные и имеют равные длины, то данные вектора не могут быть равными.
одновременно коллинеарные и имеют равные длины, то данные вектора не могут быть равными.
С) Вектора перпендикулярны, если их скалярное произведение равно нулю, поскольку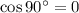 :
:
ответ: А) ни при каких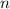 вектора
вектора 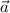 и
и 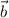 не равны; В) при
не равны; В) при 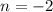 и
и 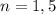 ; С) при
; С) при