При каком наименьшем натуральном “a” уравнение имеет решение.
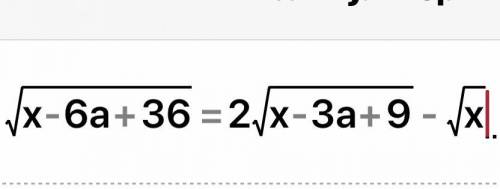
Другие вопросы по теме Математика
Популярные вопросы
- Твір-роздум на тему маленька неправда тягне за собою велику брехню...
3 - (57мин28сек+3ч56сек)*50 ответ перевести в сутки часы минуты...
1 - (57мин28сек+3часа56сек)*50 ответ пе ревести в сутки часы минуты...
3 - .(Номер машины состоит из трех цифр и может начинаться с нуля. какова рероятность...
3 - буквенные ребусы 1. ах^a=бах 2. аа^н =анна 3. как=б^к какую цифру надо поставить...
1 - .(Решить методом сложения линейного уравнения с двумя неизвестными. в двух бидонах...
2 - Почему бездушный человек опасен для окружающих?...
3 - .(Потрібно відремонтувати 140 км. дороги. за перший тиждень відремонтували 36%...
1 - .(Найдите такое десятизначное число, в котором его первая цифра обозначает общее...
1 - .(За перший місяць відремонтували 65% дороги, за другий 60% від остачі а за...
3
ответ:12
Пошаговое объяснение:
Заметим, что условие (2) строже условия (1), а условие (3) выполняется при любых a
Найдем при каких a верно (2) и (4):
Таким образом