1. Математика
  2. При каких значениях переменной

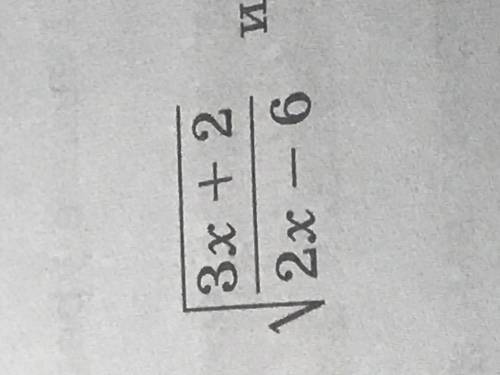
При каких значениях переменной выражение имеет смысл? (см.фото)


При каких значениях переменной выражение имеет смысл? (см.фото)

яяя489 яяя489    2   09.12.2021 22:43    0

Ответы
hitman1790 hitman1790  30.01.2022 02:44

x=(-inf;-\frac{2}{3}] и (3;inf)

(inf заменяй на бесконечность)

Пошаговое объяснение:

\sqrt{\frac{3x+2}{2x-6}}

Чтобы выражение существовало нужно чтобы:

Знаменатель был не равен нулю и

Подкоренное выражение было не меньше нуля.

Остальных условий существования для данного выражения нет.

Чтобы знаменатель не был равен нулю, 2x-6 не должно быть равно нулю.

2x-6\neq 0

2x\neq 6

x\neq 3

Значит x не равно нулю.

Следующее условие:

Чтобы подкоренное выражение не было меньше нуля,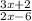 \frac{3x+2}{2x-6} не должно быть меньше нуля.

\frac{3x+2}{2x-6}\geq 0

x=(-inf;-\frac{2}{3}] и (3;inf)

(inf заменяй на бесконечность)

Находим те значения, которые НЕ походят

x\neq (-\frac{2}{3};3]

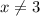В итоге мы получили, что x\neq (-\frac{2}{3};3]x\neq 3 Второе высказывание, что 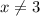x\neq 3 писать не нужно, так как из первого высказывания x\neq (-\frac{2}{3};3] это и так понятно.

Теперь из x\neq (-\frac{2}{3};3] можно понять, что x=(-inf;-\frac{2}{3}] и (3;inf).

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
keep19995 keep19995  17.09.2019 05:30
Сравни 45см или 4дм5см1мм; 20м 5дм или 205дм; 15см или 5дм 5 см; 2м 5дм или 248 см; 31м 3дм или 313дм...
averianova1986 averianova1986  17.09.2019 05:30
Хумножить на 5 плюс 495 равно 1000 у плюс 180 подарить на 6 равно 5500 (d минус 420) умножить на 2 равно 160 990 плюс а равно 3468 плюс 532...
Дария2403 Дария2403  17.09.2019 05:30
Водном лесном участке заготовили 56 бревен,а на другом 25 бревен, сколько надо грузовых машин,что бы вывести эти бревна,если каждая машина берёт по 9 бревен...
Xilolahonabdullaeva Xilolahonabdullaeva  17.09.2019 05:30
Умарата было 1600 тенге он потратил 1/4 часть этих денег на покупку марок и 3/5части на покупку альбома сколько денег осталось у марата...
про739 про739  17.09.2019 05:30
Найдите с координатной прямой сумму чисел -4 и -2,7...
666642 666642  17.09.2019 05:30
Выполните вычитание: 22,895-5,678= 2)6,07-3,4= 3)20,02-9,253....
Ymnichkaaaaaa Ymnichkaaaaaa  17.09.2019 05:30
Выполните действия а) -1,5+0,8. б) -3/5-8/9. в) 2 3/8-4...
katiatrush86 katiatrush86  17.09.2019 05:30
Найдите значение выражения -)+4+(-2,7)...
vgorelova62 vgorelova62  17.09.2019 05:30
Найдите площадь прямоугольной трапеции,если основания равны 8 см и 10 см,а боковая сторона,перпендикулярна нижнему основанию ровно 5 см...
olga000064 olga000064  17.09.2019 05:30
Сделать.. какие свойства равенств . (8c-1)•5=235 . (4n+12): 8=136...

Популярные вопросы