При каких значениях параметра kуравнение -x^2ー2kx+k^2-8=0 имеет два положительных корня? a) ( 2; (корень из 2))
б) (-2*(корень из 2);-2
в) 2*(корень из 2); +беск
с) - беск; -2 *(корень из 2)
Другие вопросы по теме Математика
Популярные вопросы
- Дан параллелограмм ABCD, ab=m, ad=n, m=середина bc. Выразите...
3 - Мәтін не туралы екенін анықтаңыз. А. Қала моншасы В. Ғылыми жобалар...
3 - Физическая единица, которая является единицей измерения скорости: *...
2 - у нас СОЧ :( Сторона АС треугольника АБС равна 28см. Сторона...
2 - В треугольнике ABC угол при вершине B прямой. Известно, что отношение...
3 - Казак адибетинен бж кимде бар ответтери отинем...
3 - Задание 2. Используя список живых организмов, составь пищевую...
3 - Стиль текста 17слова абай кунанбаев...
2 - По характеристике определи политического деятеля : Он стал известен...
3 - Найдите углы образованные при пересечении двух прямых если один...
2
k ∈ (-∞; -2) ∪ (2; +∞)
Пошаговое объяснение:
Данное уравнение (если я правильно понял):
1. Найдем дискриминант:
дискриминант СТРОГО больше нуля так как у нас должно быть ДВА корня, и мы считаем что они разные.
решаем полученное неравенство:
По теореме Виета:
Но также по условию корни положительны, тогда их сумма и произведение тоже положительны:
Находим пересечение этого множества с тем, что мы нашли ранее, тогда k ∈ (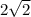 ; +∞)
; +∞)