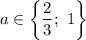При каких значениях параметра a уравнение не имеет решений?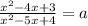
Другие вопросы по теме Математика
Популярные вопросы
- Главная тема текста и так бывает по л.киселевой...
3 - Чем являются слова выделенные слова в стихотворении лаптевой е.с.? нам...
1 - Что было результатом во время деятельности княгини ольги?...
1 - При ! найдите значения выражений ( 1 + 7\23) * ( 2 - 4\25) : ( 99 - 98...
3 - Акой признак объединяет 1)азот 2)водород 3)кислород и 4 )гелий...
2 - Від чого залежить кінетична енергія тіла...
1 - Придумай и запиши своё предложения чтобы в нём было имя собственное....
1 - Решить пример: (2n-14)(n+2). тема: умножение многочлена на многочлен....
1 - Вкаких из этих слов есть только мягкие согласные звуки ; пилить,жить,ежики,висеть,перелететь,чулочки....
2 - Скакой целью фирмы формируют новые потребности людей?...
2
Разложим числитель и знаменатель на множители:
Уравнение примет вид:
Знаменатель не может обращаться в ноль, значит:
Учитывая это, сократим дробь:
Решим уравнение:
Если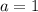 , то получим неверное равенство
, то получим неверное равенство 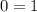 . Значит, при
. Значит, при 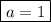 уравнение не имеет решений.
уравнение не имеет решений.
Если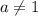 , то разделим обе части на
, то разделим обе части на  :
:
Остается выяснить, при каких значениях такая дробь дает недопустимые значения
такая дробь дает недопустимые значения 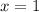 и
и 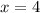 , при которых в исходном уравнении обнуляется знаменатель.
, при которых в исходном уравнении обнуляется знаменатель.
Приравняем дробь к 1:
При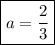 исходное уравнение не имеет решений.
исходное уравнение не имеет решений.
Приравняем дробь к 4:
Получено неверное равенство, значит этот случай не реализуется.
Окончательно получим, что при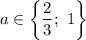 уравнение не имеет решений.
уравнение не имеет решений.
ответ: