При каких значениях параметра а уравнение будет иметь два различных отрицательных корня? Подробно Уравнение на фото!

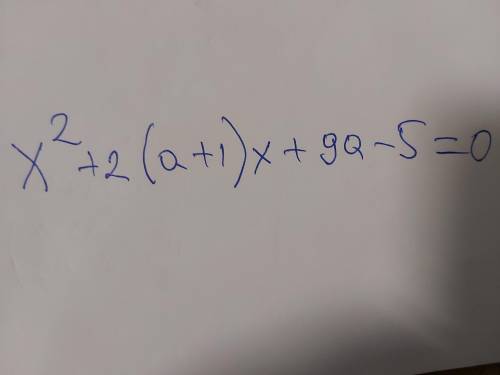
При каких значениях параметра а уравнение будет иметь два различных отрицательных корня? Подробно Ур

Ответы

lapkinalidala 28.11.2020 17:58

x^2+2(a+1)x+9a-5=0

Уравнение имеет два различных корня, если дискриминант положителен.

$D/4=(a+1)^2-(9a-5)=a^2+2a+1-9a+5=x^2-7a+6=\\\\=(a-1)(a-6)0\ \ \Rightarrow \ \ \ \underline {\ a\in (-\infty ;1)\cup (6;+\infty )\ }$

По теореме Виета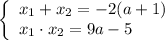 $\left\{\begin{array}{l}x_1+x_2=-2(a+1)\\x_1\cdot x_2=9a-5\end{array}\right$ . Учитывая, что оба корня

отрицательные , сумма корней отрицательна, а произведение положительно.

$\left\{\begin{array}{l}-2(a+1)0\end{array}\right\ \ \left\{\begin{array}{l}a+10\\9a5\end{array}\right\ \ \left\{\begin{array}{l}a-1\\a\dfrac{5}{9}\end{array}\right\ \ \Rightarrow \ \ a\dfrac{5}{9}$

Теперь осталось найти пересечение множеств: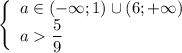 $\left\{\begin{array}{l}a\in (-\infty ;1)\cup (6;+\infty )\\a\dfrac{5}{9}\end{array}\right$ .

Параметр "а" будет принадлежать такому множеству:

$a\in \Big(\, \dfrac{5}{9}\ ;\ 1\, \Big)\cup \Big(6\, ;+\infty \Big)$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

KiraKen 20.07.2019 18:50

Изменит в каждом слове одну букву чтоб получилось название животного слово гол...

darkelan 20.07.2019 18:50

710-2=38 5-4=81 2-174 4+3=29 2+4=51 надо востановить пропушеные цифры чтоб был ответ правельный....

romankovalev21 20.07.2019 18:50

Сравните числа и запишите ответ в виде неравенства: а) 0 и -140 б) 0 и 25 в) 18 и -18 г) -31 и -310 д) 421 и 124 е) -999 и 1....

Кукарику12 20.07.2019 18:50

Вмагазин одинаковые коробки скрепок. из них 24 упаковки белых скрепок что в 3 раза больше чем цветных скрепок. определи сколько цветных скрепок если в одной упаковке 1000 скрепок....

maximfz 20.07.2019 18:50

Реши уравнения 500+a=870-70; k-200×4=100; 600÷b=250-50...

andreybober20 20.07.2019 18:50

Придумать название команды,если девиз мы помним мы гордимся...

AlyonaAn 20.07.2019 18:50

Решить по действиям подробно 38243-5769+46•402-18144: 56: 56=?...

12poli 20.07.2019 18:50

Составь программу действий и вычисли8: 1+2*7+2*7...

Kurakik 20.07.2019 18:50

1) увеличьте каждое из чисел : 0,6; 2,457; 14,0316; 56,05 в 100 раз, в 1000 раз 2) запишите в виде натуральных чисел 1) 2,3тыс; 2)1,2млн; 3)14,7тыс; 4)38,3млн; 5)629,5тыс; 6)0,8млн;...

Polllina2209 20.07.2019 18:50

От пристаней расстояние между которыми 195 км одновременна навтречу друг другу отплыли два катера. скорость 1 30 км/ч а другого 35км/ч через сколько часов они встететятся какое...

При каких значениях параметра а уравнение будет иметь два различных отрицательных корня? Подробно Уравнение на фото!

Популярные вопросы