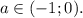При каких значениях параметра а уравнение ax^2 + (2a+1)x + 1 + a =0. имеет 2 корня разных знаков?
Другие вопросы по теме Математика
Популярные вопросы
- Какие породы слагают нижегородскую область? ♥...
1 - Вьются флаги. какой связи? (согласование,, примыкание)...
3 - От станции в противоположных направлениях отошли 2 поезда. скорость первого 75км\ч...
3 - Яке значення мають видозміни кореня і іть будь ласка! )...
3 - Вспомните особенности строения растительной клетки и объясните,каким образом и...
2 - Найдите все целые числа,удоволетворяющие неравенству: а) 0,8 |х| 4; б) 2 |х| 5,4....
2 - Надо нарисовать треугольник! 1). прямоугольный с двумя равными сторонами. 2). равнобедренным...
3 - Впараллелограмме острый угол равен фи ,а расстояния от точки пересечения диагоналей...
1 - Из двух пунктов а и в, расстояние между которыми равно 10 км, одновременно в противоположенных...
3 - Что такое общество и из каких сфер оно состаит...
2
Квадратное уравнение имеет два действительные корни, если его дискриминант больше нуля и коэффициент при х² не равен нулю, т.е.
То есть, для всех а, кроме a=0 квадратное уравнение имеет два действительных корня
Нам нужно найти такой параметр а, чтобы корни квадратного уравнения были разных знаков, то есть один положительный и один отрицательный
По теореме Виета:
_____+___(-1)___-___(0)____+____
то есть, при a ∈ (-1;0) квадратное уравнение имеет два корня разных знаков
ответ: