При каких значениях параметра а система не имеет решений:
(а+3)x+4y=3a-5
ax+(a-1)y=2
Другие вопросы по теме Математика
Популярные вопросы
- Переводчик с казахского на русский...
3 - с лабораторной работой. В дослідах нужно только уравнения написать...
2 - Вариант Сократите дроби: 1) 3x/12y = 2) (21a^8)/39a = 3) (a(x-2))/(b(x-2))...
3 - Қолдану1. Зиготаның жатыр қабырғасына бекінуі (имплантация) қалай...
1 - Айдағы жасырынбақ Мергенге жанама мінездеу керек еді...
2 - Решите неравенства: a) x^2-6x+9 0 б) -x^2+12x-36 0 СДЕЛАЙТЕ в...
2 - На рисунке изображена схема атома. Электроны обозначены черными...
1 - Знайдіть другу сторону прямокутника, якщо відомо, що одна сторона...
3 - Объясните как влияет среда обитания на эмбриогенез ящерицы крысы...
1 - Say the same in a different way...
2
ответ: -1
Пошаговое объяснение:
Если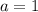
Система имеет решение
Если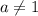
Графиком каждого уравнения системы является прямая
Система не имеет решений тогда и только тогда, когда данные две прямые не имеют общих точек
Для этого необходимо и достаточно, чтобы они были параллельны и не совпадали
Прямые параллельны в том случае, если у них равные угловые коэффициенты
Убедимся, что при найденных значениях параметра прямые не совпадают
При свободные коэффициенты равны
свободные коэффициенты равны 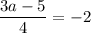 и
и 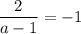 , значит при
, значит при  система не имеет решений
система не имеет решений
При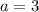 свободные коэффициенты равны
свободные коэффициенты равны 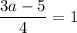 и
и 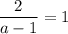 , значит при
, значит при 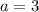 прямые совпадают и система имеет бесконечно много решений
прямые совпадают и система имеет бесконечно много решений