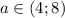При каких значениях параметра а система имеет 4 решения
Другие вопросы по теме Математика
Популярные вопросы
- Составьте и запишите предложения с 3-4 словами.обозначьте орфограмму...
1 - Жайылған кир мен шабылган шөп неге жел болғанда тез кебеді?...
2 - Почему произведение называется барышня-крестьянка?...
2 - Вмагазин привозят розы из двух оранжерей, причем из первой оранжереи...
2 - Звуковой анализ приголосних звукыв слова мудрость...
3 - Сравните 3/5 и 2/5 3/10 и 7/30 4/15 и 11/60...
3 - ответе на все вопросы 50 : 1)древнейшие люди появились на территории:...
1 - 2. решите данные уравнения. а) 2z−12=4. б) 7y−3=5−3y. 3. заданное...
2 - Напишите краткое описание характера митрофана из комедии недоросль...
2 - Дети простились с учителями. заметили щенка. сделать синтаксический...
2
Положим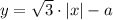 в первое уравнение системы
в первое уравнение системы
Данная система имеет ровно 4 решения, если последнее квадратное уравнение относительно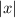 имеет два положительных корня, то есть, исходя из теоремы Виета:
имеет два положительных корня, то есть, исходя из теоремы Виета:
ответ: