При каких значениях параметр b площадь фигуры заданной системы неравенств равна 8п
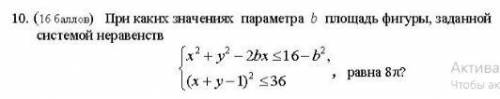
Другие вопросы по теме Математика
Популярные вопросы
- Чому, на вашу думку, історія про короля ліра завжди є актуальною?...
2 - Утворити іменники від поданих слів: завдати, зберегти, зберігати, захопити,...
2 - Завтра сдавать. радиус-вектор, определяющий положение движущейся частицы,...
3 - Put the words in the correct order and make up the sentences: often,...
3 - План монастыря святого маврикия...
2 - Написать план по тексту,, калинове намисто,, наталія дев ятко . ...
2 - Найди два числа, если известно, что утроенная разность этих чисел на...
2 - Решить . для перевозки груза требуется 12 машин грузоподъёмностью 7,5...
1 - Группы клеток, сходных по строению, функциям и обычно имеющих общее...
3 - Решите, . показатели уравнения...
2
Пошаговое объяснение:
Для начала рассмотри первое неравенство системы, оно похоже на функцию окружности. Преобразуем это неравенство и посмотрим:
Теперь рассмотрим второе неравенство системы, попробуем его преобразовать:
Из этой системы неравенств можем записать двойное неравенство:
Во втором случаем будет график прямой с штриховкой ниже данной прямой. Из всего выше сказанного про второе неравенство системы делаем вывод что графиком данного неравенства будут две прямые
будет график прямой с штриховкой ниже данной прямой. Из всего выше сказанного про второе неравенство системы делаем вывод что графиком данного неравенства будут две прямые  с штриховкой между этими прямыми. Изобразим данный график(изображение графика на рисунке ниже).
с штриховкой между этими прямыми. Изобразим данный график(изображение графика на рисунке ниже).
Теперь разберемся с первым неравенством системы: Поскольку это окружность радиуса 4, то ее площадь будет равна . Данная окружность лежит внутри прямых, где при различных значениях b мы ее можем передвигать вдоль оси абсцисс, тем самым меняя ее площадь. Необходимо указать те значения параметра b при которых площадь будет равна
. Данная окружность лежит внутри прямых, где при различных значениях b мы ее можем передвигать вдоль оси абсцисс, тем самым меняя ее площадь. Необходимо указать те значения параметра b при которых площадь будет равна  , т.е половина окружности. Отсюда становится понятно что ее площадь будет равна
, т.е половина окружности. Отсюда становится понятно что ее площадь будет равна  (т.е половине) в той точке, где прямая отсечет от нее половину.
(т.е половине) в той точке, где прямая отсечет от нее половину.
В случае с прямой , то значение параметра
, то значение параметра  , тогда окружность становится на точку -5 по оси абсцисс, где прямая
, тогда окружность становится на точку -5 по оси абсцисс, где прямая  пересекает данную окружность в двух точках, и проходит через центр (точка -5), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых
пересекает данную окружность в двух точках, и проходит через центр (точка -5), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых  , значит
, значит  решение(на рисунке ниже показана окружность при b=-5 и прямые которые отсекают нужную площадь)
решение(на рисунке ниже показана окружность при b=-5 и прямые которые отсекают нужную площадь)
В случае с прямой В случае с прямой , то значение параметра
, то значение параметра  , тогда окружность становится на точку 7 по оси абсцисс, где прямая
, тогда окружность становится на точку 7 по оси абсцисс, где прямая  пересекает данную окружность в двух точках, и проходит через центр (точка 7), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых
пересекает данную окружность в двух точках, и проходит через центр (точка 7), тогда данная прямая является диаметром окружности, соответственно делит окружность на две равные части, площадь которых  , значит
, значит  решение(на рисунке ниже показана окружность при b=7 и прямые которые отсекают нужную площадь)
решение(на рисунке ниже показана окружность при b=7 и прямые которые отсекают нужную площадь)
Получаем