При каких значениях a уравнение имеет ровно три корня?
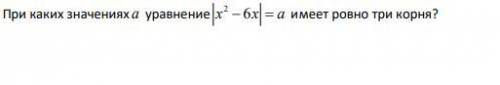
Другие вопросы по теме Математика
Популярные вопросы
- Этан → этилен → этиловый спирт → уксусный альдегид → уксусная кислота...
1 - Как вывести это r*c=р*е*е0 r - сопротивление утечки между двумя...
2 - Вкаком варианте ответа правильно указаны все цифры, на месте которых...
3 - Роль языка в жизни общество, подробно обо всем. сколько на земле...
1 - Наличие у тел потенциальной энергии объясняется: а)взаимодействием...
3 - Дан правильный шестиугольник. докажите, что если последовательно...
3 - Вкниге 63 страницы. вова прочитал 3/7 книги. сколько страниц ему...
1 - Найдите угол adc равнобедренной трапеции abcd, если диагональ ac...
2 - 1.костная ткань у миног и миксин 1) присутствует в некоторых участках...
3 - Дана арифметическая прогрессия -6; -2; 2; найти сумму первых пятидесяти...
2
a = 9
Пошаговое объяснение:
При a < 0 уравнение не имеет корней, так как значение модуля неотрицательно.
При a = 0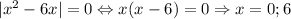 — два корня.
— два корня.
При a > 0:
Дискриминант первого уравнения: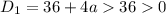
Первое уравнение в силу ограничений на a всегда имеет два корня.
Дискриминант второго уравнения: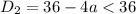
Второе уравнение может иметь два, один или ноль корней.
Если второе уравнение имеет два корня, то один из них должен совпадать с корнем первого уравнения. Это возможно при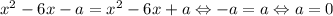 . При данном a исходное уравнение, как выяснилось ранее, имеет только два корня.
. При данном a исходное уравнение, как выяснилось ранее, имеет только два корня.
Если второе уравнение имеет один корень, то он не должен совпадать с корнем первого. Один корень уравнение имеет при дискриминанте, равном нулю: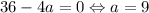 . Корень однозначно не совпадёт, поскольку совпадение произойдёт только при a = 0.
. Корень однозначно не совпадёт, поскольку совпадение произойдёт только при a = 0.
Значит, единственное значение параметра — 9.