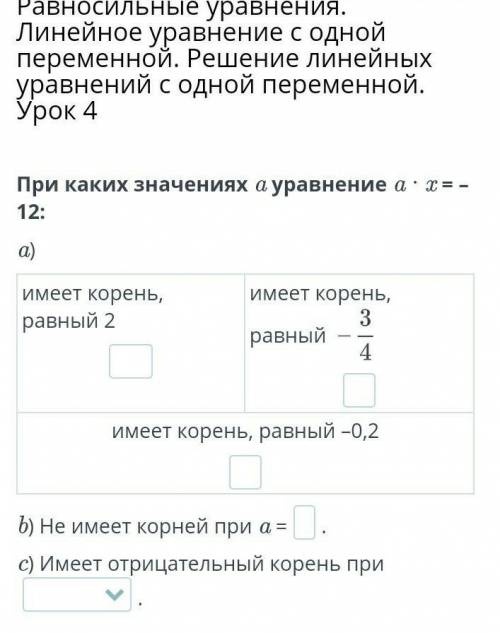
При каких значениях a уравнение a · x = –12: a)

имеет корень, равный 2

имеет корень, равный 

имеет корень, равный –0,2

b) Не имеет корней при a =.

c) Имеет отрицательный корень при 

.

а) При значении а = -6 уравнение имеет корень равный 2.

При значении а = 16 уравнение имеет корень равный -3/4.

При значении а = 60  уравнение имеет корень равный -0,2.

b) При значении а = 0  уравнение не имеет корней.

c) При а > 0 уравнение будет иметь отрицательный корень.

Пошаговое объяснение:

Требуется найти, при каких значениях а уравнение

 :

а)

1. Имеет корень, равный 2.

Подставим вместо х его значение 2 и решим уравнение относительно а:

⇒ При значении а = -6 уравнение имеет корень равный 2.

2. Имеет корень, равный .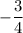

⇒ При значении а = 16 уравнение имеет корень равный .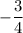

3.  Имеет корень, равный -0,2.

⇒ При значении а = 60  уравнение имеет корень равный -0,2.

b) Не имеет корней.

Уравнение не имеет решения, если при любом значении х, мы не получим верного равенства.

Это возможно только тогда, когда  а = 0.

Проверим:

⇒ При значении а = 0  уравнение не имеет корней.

с) Имеет отрицательный корень.

Правая часть у нас отрицательная.

При нахождении корня, мы делим правую часть на а. Чтобы корень был отрицательным, то а должно быть положительным.

При делении чисел с разными знаками, частное - отрицательно.

⇒ а > 0

⇒ При а > 0 уравнение имеет отрицательный корень.