При каких значениях А корни уравнения удовлетворяют условию 0
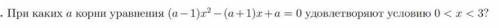
Другие вопросы по теме Математика
Популярные вопросы
- Запиши число цифрами и напиши четыре предыдущих числа. 6ед. тыс., 1ед....
1 - Выполнить синтаксический разбор. «Высоко над домом развевается красный флаг»...
2 - Конспект существование казахской нации...
2 - Орталық азия өркениетінің пайда болу факторлары...
1 - Знайти координати вектора AB- , якщо А(3;-5;0), В(-2;7;1)...
2 - Что относится к целостным и относительно устойчивым образованиям Земли естественного...
1 - 14 диагональ бар қабырға саны неше ?...
2 - Предложения со словами: язык, человек, диалог, монолог, реклама, общение,...
3 - Приведите примеры механической энергии...
3 - 0. Пользуясь таблицей интегралов, найдите: 1) ſx dx ;2) ſx Vædx ;3) [++3x²...
1
(см. объяснение)
Пошаговое объяснение:
В своем ответе я покажу два решения, каждый из которых имеет право на жизнь. Я предпочитаю решать вторым , почему и рекомендую вам начать с него.
Аналитическое решение:
При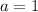 уравнение перестает быть квадратным и принимает линейный вид
уравнение перестает быть квадратным и принимает линейный вид 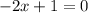 , откуда
, откуда 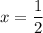 . Значит такое значение параметра нам подходит.
. Значит такое значение параметра нам подходит.
При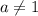 графиком уравнения является парабола.
графиком уравнения является парабола.
Корни будут, если :
:
Тогда:
По условию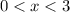 , поэтому:
, поэтому:
Решив записанную конструкцию выше имеем:
Итого ответом будет:
Достоинства подхода:
Решение "в лоб", особого ума, чтобы понять не надо.Требуются только шаблонные знания математики.Легко написать на компьютере.Недостатки подхода:
Сложные расчеты, повышающие вероятность ошибки.Ограниченность применения.Схематично-графический метод:
Заметим, что при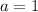 уравнение становится линейным и имеет корень
уравнение становится линейным и имеет корень 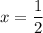 . Тогда такое значение параметра
. Тогда такое значение параметра  необходимо взять в ответ.
необходимо взять в ответ.
Дальнейшее решение выполним, когда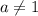 :
:
Введем функцию . Тогда
. Тогда 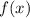 - это парабола.
- это парабола.
Изобразим эскизы возможного расположения графика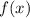 так, чтобы выполнялось условие задачи (я все делаю в единой системе координат, чтоб долго на компьютере не рисовать, вы разбейте на несколько; ситуации пронумерованы и выделены разным типом начертания).
так, чтобы выполнялось условие задачи (я все делаю в единой системе координат, чтоб долго на компьютере не рисовать, вы разбейте на несколько; ситуации пронумерованы и выделены разным типом начертания).
(см. прикрепленный файл)
Опишем эти случаи на языке математики, при условии, что выполняются фразы и
и 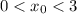 :
:
Выполним необходимые расчеты:
Тогда на условии, что![a\in\left(\dfrac{4}{5};\;\dfrac{2\sqrt{3}}{3}+1\right]](/tpl/images/2008/6422/e4b94.png) (посчитано
(посчитано  и
и 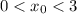 ) системы примут вид:
) системы примут вид:
Решить их не составляет труда.
Объединив найденное, получаем, что![a\in\left(\dfrac{12}{7};\;\dfrac{2\sqrt{3}}{3}+1\right]](/tpl/images/2008/6422/5f58c.png) .
.
Обратимся к записанному выше и дополним ответ:
Достоинства подхода:
Наглядное представление решения за счет создания схематичных изображений графиков.Простота вычислений.Понятность, обеспечивающая доступность понимания темы при наличии удовлетворительного уровня подготовки и желания учащегося.Недостатки подхода:
Трудно написать на компьютере.Задание выполнено!