При делении числа abc на 3 получили остаток р. Докажите,
что при делении суммы цифр это-
го числа на 3 тоже получится ос-
таток р.
Другие вопросы по теме Математика
Популярные вопросы
- Найдите и исправьте ошибки, вызванные нарушением норм . 1. среди психологов широкое...
2 - Три однакові бригади майстрів за 8 годин виготовляють 12 дерев’яних шаф. за скільки...
3 - Барабан стиральной машинке делает 120 оборотов за 1 минуту определите период и частоту...
3 - Написать диалог на , буду на подобии диалога на фото ...
1 - скласти 3 речення з словосполученнями : морська вода , шкільна подруга , шкільний...
2 - Составить план описания материка „африка”. 1. положение 2. рельеф, тектонические...
3 - Что бы определить обьем емкости неправильной формы ее сначала взвешивают затем заполняют...
2 - Уяких видах мистецтва виявився символізм? ...
1 - Составить уравнение касательной при х=1 у=(3/2х)^2/3-х^-2...
1 - 50 сочинение на тему неистребимо благородство душ по роману а. с. пушкина дубровский...
2
При делении числа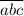 на 3 получили остаток
на 3 получили остаток 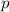 . Тогда:
. Тогда:
Распишем число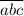 в виде суммы:
в виде суммы:
Выполним преобразования:
Так как и
и 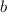 - цифры, то есть натуральные числа, то разность
- цифры, то есть натуральные числа, то разность 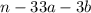 - целое число, представляющее собой неполное частное при делении суммы
- целое число, представляющее собой неполное частное при делении суммы 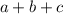 на 3. Остаток в этом случае равен по-прежнему
на 3. Остаток в этом случае равен по-прежнему 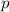 .
.