При 1/a+a=4
Найдите 1/a^3+a^3?
Примет показан и на фото вверху
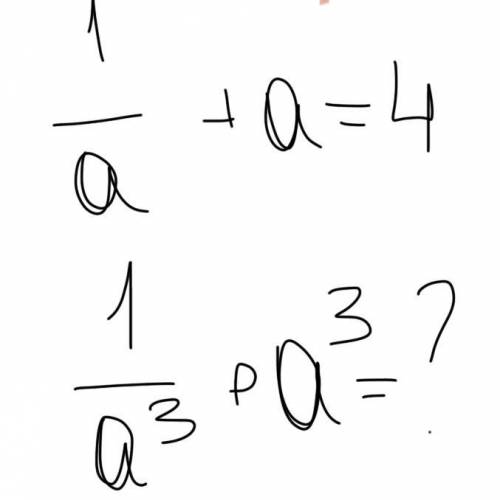
Ответы
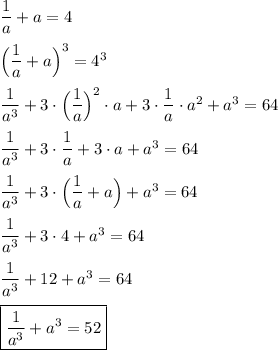
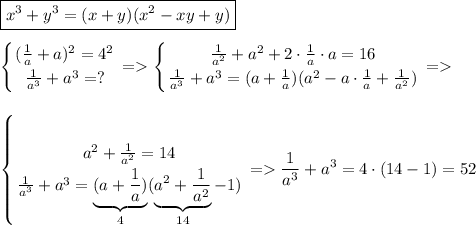
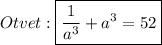
Другие вопросы по теме Математика
Популярные вопросы
- Переведите выражение многочлена у стандартному виду (a-3)7(a-3)(a+3)6a...
2 - По окр миру сделать работу над проектом! наша общая тема: мне интересно узнать...
2 - Определить возможные группы крови детей , если у матери ii ,а у отца i группа...
2 - Подскажите . 432÷4=108,480-63=417,372+108=480,189÷3=63 из этих выражений составить...
2 - Найдите объем конуса если его осевое сечения образует прямоугольный треугольник...
3 - Загадка: чёных ягод пышный кукуст хороши они на вкус...
3 - Смешали одну двадцатую кг грузинского, девятнадцать сотых кг азербайджанского...
1 - Составить сочинение по на тему море по картине дубовского,буду )...
3 - Подчеркнуть в словах буквы которые указывают на твердость предшествующего согласного...
1 - Верны ли суждения? а) меридианы можно провести через любую точку земного шара....
1