Преобразуйте в произведение: sin^2 5a - sin^2 3a
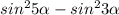
Другие вопросы по теме Математика
Популярные вопросы
- = х О дружбе, верности, любви. Г.Х. Андерсен «Снежная королева»...
3 - 1.Прочитайте статью учебника «Жанровое своеобразие и композиция...
3 - Сложные предложения N® Вариант 1 Списать, расставить знаки препинания,...
1 - Куда сместится равновесие обратимой реакции, если изменить а)...
2 - , 4 кл. Математика номер 2...
1 - Описание картины Бориса Кустодиева зимняя ярмарка...
3 - Выбери отрасль применение изображённого робота...
2 - заполнить таблицу Природные зоны Австралии. (5 колонок: 1-природная...
3 - УМАЛЮ 1 579. Мастер делает всю работу за 3 ч, что составляет...
2 - 2*(х+1)=3*(х+1)3х-5=3+3х3х+6=3*(х+2)...
2
Формула разности квадратов гласит: $a^2 - b^2 = (a + b)(a - b)$.
Применим эту формулу к выражению $sin^2 5a - sin^2 3a$.
$a = sin 5a$, $b = sin 3a$
Тогда по формуле разности квадратов:
$sin^2 5a - sin^2 3a = (sin^2 5a + sin^2 3a)(sin^2 5a - sin^2 3a)$
Теперь необходимо решить второе слагаемое $(sin^2 5a + sin^2 3a)$. Для этого мы можем использовать формулу суммы квадратов.
Формула суммы квадратов гласит: $a^2 + b^2 = (a + b)^2 - 2ab$.
Применим эту формулу к выражению $sin^2 5a + sin^2 3a$.
$a = sin 5a$, $b = sin 3a$
Тогда по формуле суммы квадратов:
$sin^2 5a + sin^2 3a = (sin^2 5a + sin^2 3a)^2 - 2(sin 5a)(sin 3a)$
Теперь мы можем заменить второе слагаемое в исходном выражении и получить:
$(sin^2 5a + sin^2 3a)(sin^2 5a - sin^2 3a) = ((sin^2 5a + sin^2 3a)^2 - 2(sin 5a)(sin 3a))(sin^2 5a - sin^2 3a)$
Таким образом, преобразование выражения $sin^2 5a - sin^2 3a$ в произведение будет выглядеть следующим образом:
$sin^2 5a - sin^2 3a = ((sin^2 5a + sin^2 3a)^2 - 2(sin 5a)(sin 3a))(sin^2 5a - sin^2 3a)$