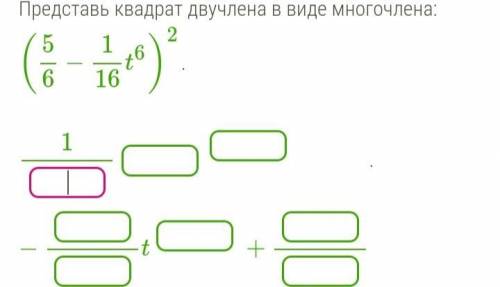
Представь квадрат двучлена в виде многочлена
(5/6-1/16t⁶)²
Другие вопросы по теме Математика
Популярные вопросы
- Вычислите наиболее удобным значение выражение: 1) 613×14+x×387, если x =14...
3 - Решить уравнение: (1+cos4x)×sin2x=cos²2x подробно, подробно, ....
1 - Почему длина ломаной больше, чем концы ломанной?...
2 - Почему дизайнеры любят применять оптические иллюзии...
1 - Лодка по течению 2,4 часа , а против 3 , 2 часа . путь , пройденный по течению...
3 - 7/6 числа равны 49 у меня получилось 42, но так же не правильно. подскажите,...
2 - Удевочки есть 8 рублей.сколько рублей ей не хватает,чтобы купить книгу за...
1 - Начертить два отрезка длина которого отрезка 6 см а второй составляет 1/3...
3 - Найдите приближенное частное 55 : 17 с точностью до 0,001...
2 - Укажите фразеологизм : мчаться во весь дух ,держать книгу, повесить полотенце,поднести...
2
Дано: (5/6 - 1/16t^6)^2
Давайте раскроем скобки и умножим двучлен сам на себя:
(5/6 - 1/16t^6) * (5/6 - 1/16t^6)
Для умножения двучлена на двучлен, мы должны умножить каждый член первого двучлена на каждый член второго двучлена. После этого сложим все полученные члены.
На первом шаге умножим первый член первого двучлена на каждый член второго двучлена:
(5/6 * 5/6) + (5/6 * -1/16t^6) + (-1/16t^6 * 5/6) + (-1/16t^6 * -1/16t^6)
=(25/36) + (-5/96t^6) + (-5/96t^6) + (1/256t^12)
На втором шаге умножим второй член первого двучлена на каждый член второго двучлена:
(-1/16t^6 * 5/6) + (-1/16t^6 * -1/16t^6)
=(-5/96t^6) + (1/256t^12)
На третьем шаге умножим третий член первого двучлена на каждый член второго двучлена:
(-1/16t^6 * 5/6) + (-1/16t^6 * -1/16t^6)
=(-5/96t^6) + (1/256t^12)
На четвертом шаге умножим четвертый член первого двучлена на каждый член второго двучлена:
(-1/16t^6 * -1/16t^6)
=(1/256t^12)
После этого просуммировать все полученные члены:
(25/36) + (-5/96t^6) + (-5/96t^6) + (1/256t^12) + (-5/96t^6) + (1/256t^12)
Далее, объединим все члены с одинаковой степенью t:
(25/36) + 2(-5/96t^6) + 2(1/256t^12)
=(25/36) - (10/96t^6) + (2/256t^12)
=(25/36) - (5/48t^6) + (1/128t^12)
Таким образом, квадрат двучлена (5/6 - 1/16t^6) записывается в виде многочлена (25/36) - (5/48t^6) + (1/128t^12)