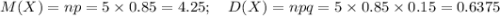1. Математика
  2. Предположим что производится обработка

Предположим что производится обработка стада животных дез составом против заболевания а, вероятность события-заболевания ликвидировано= 0,85. из стада после обработки отбирается 5 животных, требуется: 1)составить закон распределения числа здоровых животных среди n отобранных 2)а-среди 5 животных будет не более 3 животных, в- не менее 5 здоровых, с- от 3 до 4(включительно)здоровых 3) сколько здоровых животных вероятнее всего будет среди 5 отобранных 4)м(х), д(х

samira21111 samira21111    1   02.10.2019 20:10    0

Ответы
Tringt Tringt  09.10.2020 12:26

Пошаговое объяснение:

1) Составим закон распределения случайной величины X

P_5(0)=(1-p)^5=0.85^5\\ P_5(1)=C^1_5p(1-p)^4=5\times 0.85\times 0.15^4=0.00215\\ P_5(2)=C^2_5p^2(1-p)^3=\dfrac{5!}{2!3!}\times0.85^2\times 0.15^3=0.024\\ P_5(3)=C^3_5p^3(1-p)^2=\dfrac{5!}{3!2!}\times0.85^3\times 0.15^2=0.14\\ P_5(4)=C^4_5p^4(1-p)=5\times0.85^4\times 0.15=0.39\\ P_5(5)=p^5=0.85^5=0.44


2) A — среди 5 животных будет не более 3 здоровых животных

P(A)=P(k\leqslant 3)=1-P(k3)=1-C^4_5p^4(1-p)-p^5=0.16479


B — среди 5 животных не менее 5 здоровых животных

P(B)=P(k\geqslant5)=p^5=0.44


C — среди 5 животных не менее 3 и не более 4 здоровых

P(C)=P(3\leqslant k\leqslant 4)=P_5(3)+P_5(4)=0.14+0.39=0.53


3) Наивероятнейшее число k определим из двойного неравенства

np-q\leqslant k\leqslant np+p\\ 5\times 0.85-0.15\leqslant k\leqslant50\times0.85+0.85\\ 4.1\leqslant k\leqslant5.1\\ k=5

5 здоровых животных вероятнее всего будет среди 5 отобранных.


4) M(X)= np = 5\times0.85 = 4.25;~~~ D(X)=npq=5\times0.85\times 0.15=0.6375


Предположим что производится обработка стада животных дез составом против заболевания а, вероятность
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
xokkey1 xokkey1  26.09.2019 02:40
Решить 3 рiвняння : 1) 1,2x + 0,4x + 4 = 5,2 2)1,8x + 4,6x - 0,6 = 1 3)14,24x - 12,39x - 0,169 = 0,09....
Danika02 Danika02  26.09.2019 02:40
Степашка с филей приготовили 8 литров морса с трехлитровой и пятилитровой банок они разлили весь этот морс поровну. как они смогли это сделать. как сделать решением?...
kudryavcevanat kudryavcevanat  26.09.2019 02:40
Марійка посадила 55 саджанців квітів. серед них чорнобривців стільки ж, скільки й петуній, а сальвій - у 3 рази більше, ніж чорнобривців. скільки саджанців квітів кожного виду...
228alex777 228alex777  26.09.2019 02:40
6^3х+4=36 укажите промежуток содержащий корень уравнения...
fan211 fan211  26.09.2019 02:40
Одной из самых маленьких бабоочек в мире считается синий карлик.а самой считается павлиний глаз.известно,что размах крыльев у синего карлика 1,4 см,а размах крыльев павлиньего...
Terbull Terbull  26.09.2019 02:40
Указать координаты точки пересечения графиков функции y=-0,5x+2 y=3+2x...
Aleksandra1111117 Aleksandra1111117  26.09.2019 02:40
Раскрыть скобки и вычеслить 3,6 - (-1,9 + 3,6)...
4кпнигш 4кпнигш  26.09.2019 02:40
Решите в две пекарни 250 мешков муки. одна пекарня получила 10125 кг,а вторая на 1500 кг меньше . сколько мешков муки получила каждая пекарня ?...
GGG1771 GGG1771  26.09.2019 02:40
)можете кто-нибудь мне с округлением десят. дробей, !...
Сонька766 Сонька766  26.09.2019 02:40
Решите уравнение 1,4÷(0,6х-0.16)=5,5...

Популярные вопросы