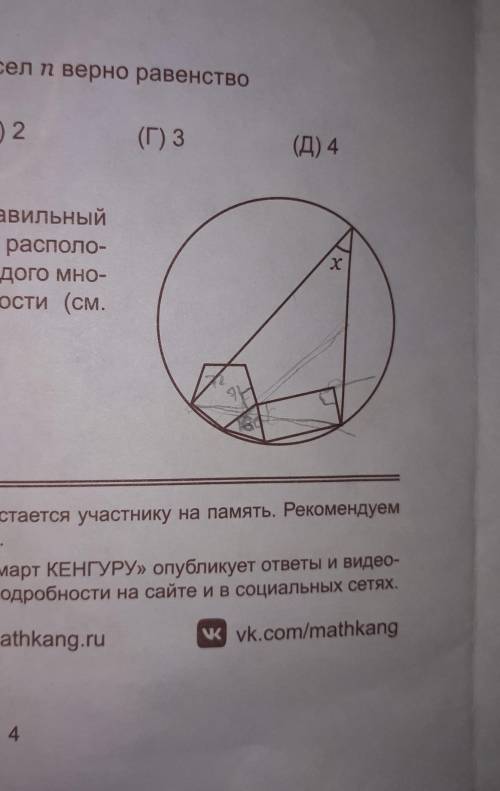
Правильный пятиугольник, правильный треугольник и прямоугольник расположены так, что две вершины каждого многоугольника лежат на окружности. Чему равен угол x? А 30° Б 36° В 40° Г 42° Д невозможно определить
Другие вопросы по теме Математика
Популярные вопросы
- Колесо на расстоянии 285 м сделало 120 оборотов. Найди диаметр колеса...
3 - У всіх реченнях підкреслити граматичні основи і написати вид речення...
2 - Одноклассники работают с текстом. Данил сохранил текстовый документ...
2 - Card 1. 1) He hasn t forgotten his Spanish since/for he left Cuba....
3 - Диск радиусом 0,2 м и массой 3 кг вращается под действием касательной...
1 - 1. Уважно розгляньте запропоновані вчителем пагони. Знайдіть верхівкові...
2 - : I like shopping. When I get my pocket money, I always spend it on...
2 - Для моллюсков характерно: 1)бесполое размножение2) кожная складка-мантия3)...
3 - Подчеркнуть все подлежащее и сказуемые определить у сказуемоемого...
3 - Можно ли найти силу зная только координаты в трех мерном пространстве,...
2
ответ: 36
Пошаговое объяснение:
Хорды, являющиеся сторонами правильных треугольника и пятиугольника, образуют угол равный
60° + 108° = 168°.
Это вписанный угол, значит, он опирается на дугу, равную
2*168° = 336°
и, значит, сумма дуг, на которые опираются стороны правильных треугольника и пятиугольника, равна
360° - 336° = 24°.
Хорды, являющиеся сторонами правильных треугольника и пятиугольника, равны. Значит, стягиваемые ими дуги равны
24°/2 = 12°.
Хорды, являющиеся стороной правильного треугольника и стороной прямоугольника, образуют угол, равный
60° + 90° = 150°.
Это вписанный угол, значит, он опирается на дугу, равную
2*150° = 300°
и, значит, сумма дуг, на которые опираются сторона правильного треугольника и сторона прямоугольника, равна
360° - 300° = 60°.
Таким образом, сумма всех дуг, на которые опирается искомый вписанный угол
12° + 60° = 72° и, значит,
х = 72°/2 = 36°.
ответ (Б) 36°.