Правильная шестиугольная пирамида. угол между боковой гранью и основанием - 30 градусов. площадь боковой поверхности - 300. найти объём пирамиды.
Другие вопросы по теме Математика
Популярные вопросы
- Бамсы байрақты Дерсеханұлы Бұқашпен салыстырыңдар...
1 - 2. Объём газа V = 0,1 м, дав- ление р= 10° Па. При изотер-мическом...
3 - висота трикутника ділить один із його кутів на кути, що дорівнюють...
2 - Какой путь пешеход если он шёл 3 часа со скоростью u км/ч и 2 часа...
3 - 18. Вычислите значение выражения x+y при х=–2;y=3,n=4...
1 - Скажите какие изобретения выросли из шестерёнки...
1 - с Геометрией В 17:00 сдавать ...
1 - Назови и запеиши числа в порядке возрастания в которых 2 дес.3 ед....
1 - Мәтіндегі қою қаріппен жазылған сөздердің мағынасын анықтап, тіркескен...
3 - С кем из героев встречался Геракл когда совершил 12 подвиг...
3
Пошаговое объяснение:
"Как видите, ни один из элементов формулы нам пока не известен. Нужно выразить их из данных условия, т.е. через площадь боковой поверхности пирамиды."
Так как основанием пирамиды является правильный шестиугольник, то
Учитывая, что угол между боковой гранью и основанием равен 30°, то апофема и высота пирамиды относятся, как, соответственно, гипотенуза и меньший катет в прямоугольном треугольнике, т.е.
Найдём отношение площади боковой поверхности Sb. и площади основания Sо. Каждая из поверхностей раскладывается на 6 равных треугольников.
Площадь бокового треугольника равна
Площадь треугольника основания равна
a*cos(30°)=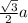 ).
).
Значит отношение площади боковой поверхности и площади основания равно:
Тогда площадь основания So можно выразить через площадь боковой поверхности как:
Теперь, чтобы найти высоту пирамиды, нужно выразить апофему а через площадь боковой поверхности Sb.
Основание - правильный шестиугольник, состоит из 6 правильных треугольников с внутренними углами по 60°. Высоту такого треугольника мы уже находили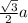 . Такая высота (являясь также биссектрисой) делит правильный треугольник на 2 прямоугольных с прилежащим к ней углом 30° (60°/2=30°).
. Такая высота (являясь также биссектрисой) делит правильный треугольник на 2 прямоугольных с прилежащим к ней углом 30° (60°/2=30°).
Тогда сторона b правильного треугольника равна
b=a.
Подставив полученные выражения в формулу боковой поверхности, получим:
а так, как мы вывели, что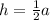 , то
, то
Теперь все неизвестные выражены через площадь боковой поверхности и мы можем вычислить объём пирамиды:
*в решении задачи многократно применялась теорема Пифагора. Чтобы сократить текст решения, я это опустил.