Пр49) Касательная, проведенная к графику функции y= корень (1,44- x^2) , пересекает ось абсцисс в точке (-2;0) .Найдите уравнение касательной . Заранее

Другие вопросы по теме Математика
Популярные вопросы
- Сделать морфемный разбор слов: пасынок, правнук, сумрак, бивень, болезнь,...
2 - Разобрать слово выпустили на приставку корень окончание...
3 - В2009г. семья петровых платила за коммунальные услуги 920р. в 2010г. стоимость...
1 - Выпиши из предложения в которых предано: 1)чувство долгожданной радости...
2 - Найдите простые разделения смеси бытового мусора, состоящего из поваренной...
3 - Напишите уравнение электролитической диссоциации h2so4,hno3,koh,ca? (oh)2,agno3,k3po4,na2so4...
2 - Маленькое сочинение которое начинается в один из осенних дней мы отправились...
1 - На дорогу от посёлка до города на грузовой машине не потребуется 48 л бензина.хватит...
3 - Вравнобедренной трапеции основания = 3 см и 5 см, а боковая сторона -7см....
2 - Нужно составить по 2 предложения на каждое время....
2
Касательная имеет вид :
Составим ее :
В точке (-2 ; 0) :
{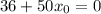
{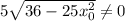
-------------------------
{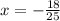
{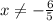
{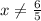
-------------------------
-------------------------
Касательная :
ответ : A)
Данная точка (-2;0) не является точкой касания, т.к. в этой точке функция не определена. Пусть у точки касания абсцисса равна а.
Значение функции в точке а равно f(a)=√(1.44- a²) ,
производная функции равна f'(x)=-2х/(2√(1.44-х²)=-х/√(1.44-х²);
f'(а)=-а/√(1.44-а²);
Уравнение касательной у=√(1.44- a²)-(а/√(1.44-а²))*(х-а);
Касательная проходит через точку (-2;0), следовательно, ее координаты удовлетворяют уравнению касательной
√(1.44- a²)-(a/√(1.44-а²))*(-2-а)=0; а≠±1.2; 1.44- a²-а*(-2-а)=0;⇒
а=-0.72∈(-1.2;1.2) вне этого интервала подкоренное выражение меньше нуля или равно нулю.
Уравнение искомой касательной
у=√(1.44- 0.72²)-(-0.72/√(1.44-0.72²))*(х+0.72);
у=0.96+(0.72/0.96)*(х+0.72);
у=0.96+0.75*(х+0.72);
у=0.96+0.75х+0.54;
у=0.75х+1.5.
Верный ответ А) у=3х/4+3/2