Пр26) Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=log2(х) , параллельной прямой, проходящей

Question

Математика: Пр26) Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=log2(х) , параллельной прямой, проходящей через точки A(1; 0) и B(2; 1) . Заранее

NastyaVait3 · Answer

Найдем уравнение прямой, параллельной касательной к графику функции .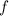

Прямая, проходящая через точки A(x₁, y₁) и B(x₂, y₂), представляется уравнением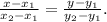 $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}.$ . Подставляем все данные в условии значения и получаем:

$\frac{x-1}{2-1}=\frac{y-0}{1-0};\\\\y=x-1$

(Отмечу, что уравнение можно было найти и без этого уравнения. Запишем уравнение в виде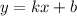 y=kx+b . Поскольку точки А и В принадлежат прямой, то выполняется система 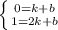$\left \{ {{0=k+b} \atop {1=2k+b}} \right.$ . Решая эту систему получаем, что 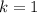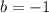k=1 , b=-1 , т.е. уравнение прямой -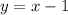 y=x-1

Угловой коэффициент заданной прямой равен коэффициенту перед x, т.е. 1. Поскольку у параллельных прямых угловые коэффициенты равны, то угловой коэффициент касательной также равен 1.

ОТВЕТ: 1.

Пр26) Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=log2(х) , параллельной прямой, проходящей через точки A(1; 0) и B(2; 1) . Заранее

Популярные вопросы