, пожайлуста. Найти экстремумы(max,min) функции.
y=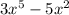
Другие вопросы по теме Математика
Популярные вопросы
- Как называют части прямой, на которые её делит любая точка этой прямой?...
2 - Порядок вычисления 21: 3*6-(18+14): 8, 63: (3*3)+(8*7-2): 6...
1 - 7определите связи предложений в тексте (цепная или параллельная)....
3 - Довести що будова тканин відповідає своїм функціям...
1 - Вежливые слова используемые при встрече...
1 - Как правильно писать чудесное или чудестное...
1 - Мелихова язык 3 класс №26 меняй подлежащее или сказуемое, что бы получилось...
1 - Решить пример 1,2 - 6,9 умножить на 1/3...
1 - Напишите мини сочинение по пословице тише едешь дальше будешь...
1 - Что обозначает цифра 2 над словам и сто нужно делать с этим словом...
3
Экстремумы в точках 0 и (2/3)^(1/3). В первой локальный максимум во второй локальный минимум.
Пошаговое объяснение:
Производная в экстремальных точках равна 0.
Производная функции
15x^4-10x=5x*(3x^3-2)
В точках x=0 и х=(2/3)^(1/3) (корень кубический из 2/3) производная равна 0.
Чтобы выяснить локальный максимум или локальный минимум в этих точках можно взять вторую производную
Вторая производная 60x^3 -10 в 0 отрицательна, значит в этой точке локальный максимум.
При х=(2/3)^(1/3) вторая производная положительна (равна 110)
Значит в этой точке локальный минимум.
То же самое можно было бы сделать просто посмотрев на чередование знаков производных
+ при х меньше 0.
- на интервале (0,(2/3)^(1/3) )
+ при х больше (2/3)^(1/3)