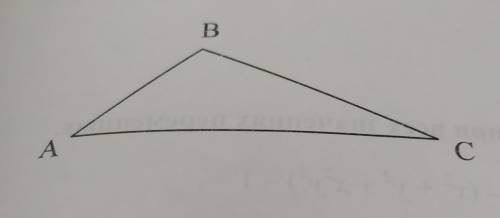
Постройте серединный перпендикуляр к сторонам BC и AC треугольника ABC

Для построения серединного перпендикуляра к сторонам BC и AC треугольника ABC, нам понадобятся следующие инструменты и шаги:

Инструменты:
- Линейка
- Карандаш
- Компас

Шаги:

1. Назовем середины сторон BC и AC как D и E соответственно. Для этого, проведите отрезки CD и AE, которые проходят через середины сторон BC и AC соответственно.

2. Теперь возьмите компас и установите любой радиус, который больше половины длины стороны BC. Чтобы выполнить это точно, измерьте длину стороны BC с помощью линейки, разделите полученную длину пополам и установите эту половину в компасе.

3. С центром в точке D, нарисуйте дугу, используя компас. Убедитесь, что эта дуга пересекает отрезок CD.

4. С центром в точке E, нарисуйте другую дугу, используя тот же радиус. Убедитесь, что эта дуга пересекает отрезок AE.

5. Обозначьте точки пересечения дуг как F и G, соответственно.

6. Соедините точки F и G линией. Эта линия будет серединным перпендикуляром к сторонам BC и AC.

Пояснение:

Построение серединного перпендикуляра основано на свойствах треугольника, в частности на том, что середины сторон треугольника соединены внутренними биссекторами каждого угла.

Серединный перпендикуляр к стороне BC будет проходить через середину этой стороны (точка D) и быть перпендикулярным к ней. Аналогично, серединный перпендикуляр к стороне AC будет проходить через середину этой стороны (точка E) и быть перпендикулярным к ней. Таким образом, точки пересечения перпендикуляра через стороны BC и AC будут находиться на середине этих сторон (точки F и G соответственно).

Решение, описанное выше, является способом построения перпендикуляра, используя компас и рулетку. Он гарантирует точный результат и позволяет получить серединный перпендикуляр, который разделит стороны BC и AC пополам и будет перпендикулярен им.