Построй график самостоятельно,и определи,какими свойствами обладает каждая из
функций:
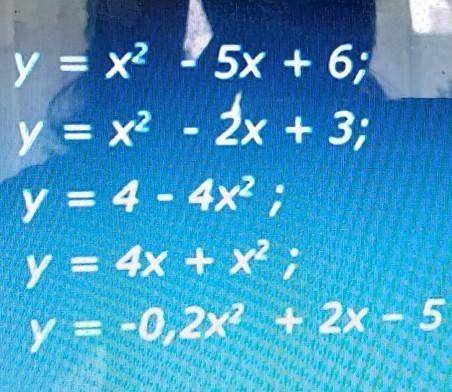
Другие вопросы по теме Математика
Популярные вопросы
- Хозяйственная деятельность человека не может к а) загряению б)...
3 - Цена акции за неделю понизилась на 10 % и стала равной 3.р 60к...
1 - Високе величне хвойне дерево з товстим стовбуром. не боїться вогню,...
1 - Спишите словосочетания,вставляя пропущенные буквы.опеределите...
2 - Вычеркните дишнее 1.na 2.mg 3.al 4.si какая из следующих групп...
3 - Определите,к каким относятся эти местоимения: что-то,это,её,свою,своей,его,все....
1 - 12см: 3= 2дм+3см= 4см*4= 12см: 3см= 1дм-3см= 5*2дм= 12см-3см=...
2 - Почему слово кедровка пишется через е?...
3 - Нужно там где стоят точечки вставить что нибудь нужное по смыслу....
2 - X^2+11x+30/3х-15 : х+5/х-5 выполните действия....
2
Для построения графика, нам необходимо знать несколько ключевых элементов. В данном случае, заданы три различные функции: f(x), g(x) и h(x). Каждая функция имеет свою формулу, которая указывает на способ вычисления значения функции для каждого значения переменной x. Давайте рассмотрим каждую функцию по отдельности и проанализируем ее свойства.
1) Функция f(x) = 2x + 3.
Для построения графика этой функции, нам необходимо выбрать несколько значений x, вычислить значение f(x) для каждого из них и отметить полученные точки на плоскости. Для наглядности, можно выбрать несколько значений для x и построить таблицу соответствия:
x | f(x)
-------------
-2 | -1
0 | 3
1 | 5
2 | 7
Теперь, отметим полученные значения на графике. Для этого, нарисуем оси координат и отметим точки с координатами (-2,-1), (0,3), (1,5) и (2,7). Затем, проводим прямую через эти точки.
Свойства функции f(x):
- График представляет собой прямую линию.
- Значения функции растут с увеличением значения переменной x.
- Угловой коэффициент равен 2, что означает, что значение функции увеличивается на 2 при увеличении значения x на 1.
- Свободный член (3) указывает, что график функции пересекает ось y в точке (0,3).
2) Функция g(x) = -x^2 + 4.
Для построения графика этой функции, мы последовательно выбираем значения x, вычисляем соответствующие значения g(x) и отмечаем точки (x, g(x)) на графике.
Давайте построим таблицу соответствия, выбрав несколько значений для x:
x | g(x)
---------------
-2 | 0
-1 | 3
0 | 4
1 | 3
2 | 0
Отмечаем полученные значения на графике. Для этого, рисуем оси координат и отмечаем точки с координатами (-2,0), (-1,3), (0,4), (1,3) и (2,0). Затем, проводим плавную кривую линию через эти точки.
Свойства функции g(x):
- График представляет собой параболу, выпуклую вниз.
- Максимальное значение функции равно 4, достигается при x = 0.
- Значения функции убывают при увеличении или уменьшении значения x.
- Вместе с тем, функция имеет симметрию относительно оси y.
3) Функция h(x) = -2.
Данная функция имеет постоянное значение -2 независимо от значения x. То есть, для любого значения x, функция h(x) всегда будет равна -2.
Чтобы построить график такой функции, мы рисуем горизонтальную прямую на уровне y = -2. Это означает, что график функции h(x) будет представлять собой горизонтальную прямую линию, проходящую через значение -2 на оси y.
Свойства функции h(x):
- График представляет собой горизонтальную прямую линию.
- Значение функции постоянно и всегда равно -2 независимо от значения x.
Надеюсь, что данное объяснение поможет тебе лучше понять, как построить график и анализировать свойства различных функций. Если у тебя есть еще вопросы, не стесняйся задавать!