Построить область плоскости z определяемую данными неравенствами
 }^{3} \leqslant (z - \overline{z}) ^{2} )
Другие вопросы по теме Математика
Популярные вопросы
- Изучение уровня воспитанности человека на основе анализа содержания высказываемых...
2 - Использование своего служебного положения в личных целях, – это негативная...
2 - Высший уровень развития групповой деятельности, – это коллективная деятельность...
1 - Объяснение результатов исследования называется интерпретация экстраполяция...
3 - Раздел психологии, изучающий особенности психики разных возрастных групп,...
2 - Система предложенных наукой и проверенных практикой алгоритмов и средств,...
1 - Организация учебных занятий, которая предполагает создание под руководством...
3 - Верны ли определения? А) Дошкольный возраст – это этап психического развития,...
3 - Верны ли утверждения? А) В условиях педагогического процесса предметом задачи...
3 - Верны ли утверждения? А) В результате усложнения и увеличения числа движений...
2
Положим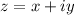 , тогда
, тогда 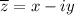 . Имеем
. Имеем
Левая часть неравенства всегда неотрицательно, поэтому последнее неравенство имеет место только при x = y = 0
Построить область плоскости z не проблема, это точка (0;0)