Постойте взаимно однозначное отображение отрезка [0;1] на полуинтервал [0;1). С объяснением
Другие вопросы по теме Математика
Популярные вопросы
- К непереходным глаголом относится 1) решать, поощрять 2) Открыть, чувствовать3...
3 - Прочитайте слова. Распределите по группам слова, обозначающие: а) толерантное...
1 - Написать небольшое сочинение - эссе по произведению М.П.Мусоргского Богатырские...
3 - Движение какого тела можно считать равномерным...
3 - Решите уравнение, с решением 2x^4+x^3-9x^2-4x-4=0...
3 - при спаоюванні 1.2л органічної речовини ожержали 4.8л со2 укаж кількість...
1 - Сравнить толкования слова нигилист , данные Николаем Петровичем и Павлом...
2 - 1. Написати твір, використавши всі види речень за метою висловлювання та...
3 - Для сокращённого иного уравнения H2s + Cu+2 — CuS + 2H+ привести два полных...
2 - Установите соответствие между примерами и видами потребностей, к которым...
1
Обозначим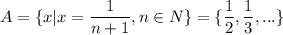 - очевидно, счетное множество. Заметим, что
- очевидно, счетное множество. Заметим, что ![A\subset [0;1],A\subset [0;1)](/tpl/images/1375/5316/67b0e.png) , при этом
, при этом ![[0;1]\backslash (A\cup \{1\})=[0;1)\backslash A](/tpl/images/1375/5316/937d3.png) . Тогда элементы множества
. Тогда элементы множества 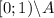 можно отразить на самих себя, и при этом построить взаимно однозначное отображение счетного множества
можно отразить на самих себя, и при этом построить взаимно однозначное отображение счетного множества 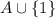 на А
на А
Построим отображение![f:[0;1]\to[0;1)](/tpl/images/1375/5316/c8ba7.png)
При этом, очевидно, разные элементы![[0;1]](/tpl/images/1375/5316/90495.png) переходят в разные элементы
переходят в разные элементы 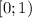 , и при этом, очевидно, для каждого элемента [0;1) существует прообраз в [0;1], т.е. существует и обратное отображение
, и при этом, очевидно, для каждого элемента [0;1) существует прообраз в [0;1], т.е. существует и обратное отображение ![f^{-1}:[0;1)\to[0;1]](/tpl/images/1375/5316/2de33.png)
А значит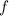 - искомая биекция
- искомая биекция