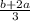Последовательность

определяется рекуррентным соотношением

при n≥1 и начальным условием

найдите

Другие вопросы по теме Математика
Популярные вопросы
- 2.придумать свою ситуацию, где присутствует 1 модель 3.придумать свою ситуацию,...
3 - Вчем биологический смысл смерти организма?...
1 - Найдите область определения функции 2вар....
2 - Сочинение по произведению нины сергеевны дешевской бруно.это сказка или рассказ?...
3 - Кого можно назвать фаталистом в герое нашего времени, не менее 200 слов, и...
1 - Составьте сюжет,чтобы по нему можно было написать лирическую песню....
2 - Тело массой 1кг скользит по горизонтальной шероховатой поверхности. коэффициент...
2 - Нужно по этой таблице (1 пример) составить тоже самое, только с другой ситуацией!...
2 - Подряд выписаны все натуральные числа 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,...
3 - 11 класс 30 электрон влетает в магнитное поле со скоростью 20 000 км/с и движется...
1
Введем координатную прямую с началом в точке 0, точки a и b (пусть b>a) и кузнечика, сидящего в точке 0. Каждый раз он будет прыгать в точку, соответствующую следующему члену. Сначала он прыгнет в середину отрезка (a, b). Затем он прыгнет в середину правой середины, затем в середину левой середины и так далее. Пусть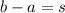 , тогда модуль длины n-ого прыжка кузнечика будет равен
, тогда модуль длины n-ого прыжка кузнечика будет равен 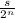 ; Теперь можем считать:
; Теперь можем считать: 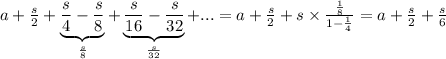 ; В итоге:
; В итоге: 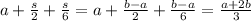 . Если же a>b, то предел равен
. Если же a>b, то предел равен