понять как решать этот предел. При обычной подстановке нуля под x получается ответ 1. Однако все онлайн-калькуляторы выдают ответ 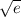$\sqrt{e}$ . Почему?

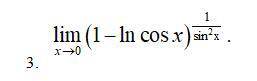
понять как решать этот предел. При обычной подстановке нуля под x получается ответ 1. Однако все онл

Ответы

Tukko 06.02.2021 13:59

Пошаговое объяснение:

1. просто подставлять х=0 нельзя, потому как в степени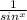 $\frac{1}{sin^x }$ знаменатель превращается в 0

решается через второй замечательный предел

$\lim_{x \to 0}(1+\frac{a}{x} )^{bx} = e^{ab}$

$\lim_{x \to 0} (1-ln(cosx))^{1/sin^2x} =$ ( sinx ≈ x) =

$\lim_{x \to 0} (1-ln(cosx))^{1/x^2}= \lim_{x\to 0} a_n (1-ln(cosx))^{\frac{-ln(cosx))}{x^2} =$

$=\left[\begin{array}{ccc} \lim_{x \to 0}(-\frac{ln(cosx)}{x^2} =\frac{1}{2} \\\\\end{array}\right] =e^{1/2} = e^{\sqrt{x} }$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

НикитаГоровой 11.05.2021 19:05

Вычислите 2223 : (535-535)²...

ElyalyaЗ 11.05.2021 19:04

paschprudnikov 11.05.2021 19:04

metior 11.05.2021 19:04

KoRiiZa 11.05.2021 19:04

yuyornevzkoxkdhd543 11.05.2021 19:03

решить уравнение: а)4(х-6)+22=-14 б) 2,8-0,7d=-3,5...

Евгений112576 11.05.2021 19:03

можно сразу решение и ответ я вам ...

Vitaly536218 11.05.2021 19:03

asimagasanova 11.05.2021 19:03

dilyahashimova 29.07.2019 07:30

понять как решать этот предел. При обычной подстановке нуля под x получается ответ 1. Однако все онлайн-калькуляторы выдают ответ . Почему?