Пользуясь правилом Лейбница найдите ..., если...
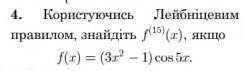
Другие вопросы по теме Математика
Популярные вопросы
- 183. Вычислите. а) 25 + 2[12 - 3 (11 – 7)] =b) (15 – 4 (12 - 9)] + 40 =c) 51...
3 - Write the correct form of the verb to be: 1. He a doctor. 2. I a football player....
2 - Якщо пряма перетинає одну з двох паралельних прямих то вона перетинає й іншу...
2 - 17.Установіть відповідність між героями «Слово про похід Ігорів» та їхніми репліками...
2 - Напишіть рівняння реакцій добування а) метанолу, б) етанолу, в) пропан-1-олу...
3 - Плотность золота 19300 кг/м3. Выполнить перевод в г/см3. Определить плотность...
2 - Педагогический ситуации по разрешению конфликтов ...
2 - Қазақстан елордасы-Астана эссе қандай...
2 - Напишите молекулярная и полное сокращенные уравнение реакции...
3 - Қай өлеңінде Сүйінбайн бір өнірдің атқа мінерлерінын әділетсіздігін аитады...
3
ответ: 630*[-5^13*sin(5*x)]+90*x*[-5^14*cos(5*x)]+(3*x²-1)*5^15*sin(5*x)
Пошаговое объяснение:
Пусть u(x) и v(x) - дифференцируемые функции от x. По правилу Лейбница, [u*v](n)=C(n,k)*u(n-k)*v(k), где C(n,k) - число сочетаний из n по k. В нашем случае u=3*x²-1 и v=cos(5*x), поэтому u(3)=u(4)=...=u(15)=0, и тогда [u*v](15)=C(15,13)*u"*v(13)+C(15,14)*u'*v(14)+C(15,15)*u*v(15). Но u'=6*x, u"=6, C(15,13)=105, C(15,14)=15, C(15,15)=1. Используем рекуррентную формулу для cos(m*x): [cos(m*x)](n)=m^n*cos(m*x+π*n/2). В нашем случае m=5, n=13,14,15. Тогда [cos(5*x)](13)=5^13*cos(5*x+13*π/2)=-5^13*sin(5*x), [cos(5*x)](14)=5^14*cos(5*x+14*π/2)=-5^14*cos(5*x), [cos(5*x)](15)=5^15*cos(5*x+15*π/2)=5^15*sin(5*x). Отсюда [u*v](15)=105*6*[-5^13*sin(5*x)]+15*6*x*[-5^14*cos(5*x)]+1*(3*x²-1)*5^15*sin(5*x)=630*[-5^13*sin(5*x)]+90*x*[-5^14*cos(5*x)]+(3*x²-1)*5^15*sin(5*x)