Положительные числа x и y таковы, что xy=50. Найдите наименьшее возможное значение выражения (x/2)+y. В этой задаче пришел к тому, что xx+yy( *-знак умножения) больше или равен 100. Это как подсказка. ответ дать с полным объяснением, а не просто сказать ответ!

Ответы

taylakova090820 15.10.2020 16:09

$\displaystyle\\xy = 50\\x/2+y = \frac{x}{2} + \frac{50}{x} = \frac{1}{2}\left(x+\frac{100}{x}\right)$

Найдем минимум выражения в скобках. Заметим что положительный x можно представить в виде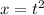 x = t^2

$\displaystyle\\t^2+\frac{100}{t^2} = t^2 - 20 + \left(\frac{10}{t}\right)^2+20 = \left(t-\frac{10}{t}\right)^2+20$

Отметим, что получившееся выражение не может быть меньше 20, а значение 20 достигается при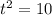 t^2 = 10 то есть при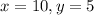 x = 10, y =5

И минимальное значение исходного выражения составляет 10/2 + 5 = 10

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

123456351 08.10.2019 17:11

Выполни сам, попроси проверить друга...

ВерочкаЛатушкина 08.10.2019 17:11

nekish21 08.10.2019 18:20

makskos4444 08.10.2019 18:20

uhudongoair 08.10.2019 17:11

Елена5616 08.10.2019 18:20

Найти градиент функции u=ln(x^2+y^2+z^2)...

юлия1657 08.10.2019 17:12

Высшая ) необходима с решением...

istomina2000 08.10.2019 17:12

Сделай вычисления по действиям...

EnoTProKoP 08.10.2019 17:12

Элиза12098 08.10.2019 18:20

Как записать сокращено b + b + b, + b, + b? ...